I have a valid proof for the Chain Rule, however I do not understand why the 'arguement' given here is incorrect.
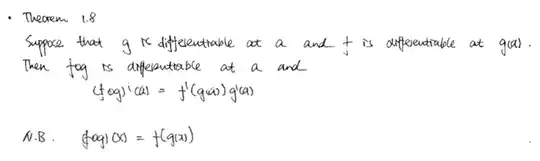

I have a valid proof for the Chain Rule, however I do not understand why the 'arguement' given here is incorrect.
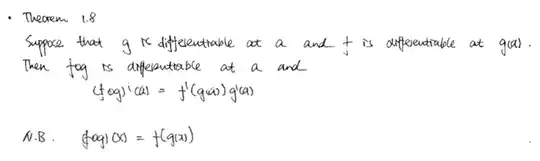

One simple way to fix the problem of "division by zero" when $g(x)-g(a)=0$ is to define the continuous function $$ \frac{\Delta f}{\Delta g}(x)= \begin{cases} f'(g(a))&\quad\text{if }g(x)-g(a)=0\\ \\ \dfrac{f(g(x))-f(g(a))}{g(x)-g(a)}&\quad\text{otherwise} \end{cases} $$ and confirm (think it through properly) that we have $$ \frac{f(g(x))-f(g(a))}{x-a}=\frac{g(x)-g(a)}{x-a}\cdot\frac{\Delta f}{\Delta g}(x) $$ both for values of $x$ where $g(x)-g(a)=0$ and other values of $x$. In the first case, both sides becomes zero, and in the second case we are basically considering the dangerous step $$ \frac{f(g(x))-f(g(a))}{x-a}=\frac{g(x)-g(a)}{x-a}\cdot\frac{f(g(x))-f(g(a))}{g(x)-g(a)} $$ which is now legitimate since $g(x)-g(a)\neq 0$. When taking limits, you will need the continuity of $\dfrac{\Delta f}{\Delta g}(x)$.
The problem is simply that if $g$ were constant in a neighborhood of $a$, then $g(x)-g(a)=0$ when $x$ is close to $a$, and thus you are dividing by $0$.
I see that this is an old post, but I'm hoping I might get a response here anyway. As I'm working through this proof, I actually don't see why we need to define Δ/Δ to be a continuous function. It seems to me both that (i) Δ/Δ is always going to be equal to the difference quotient regardless of what value we assign to it in the case that g(x) = g(a) and (ii) the limit of Δ/Δ will always approach ′(()) as x approaches a, so I don't see the harm in choosing any arbitrary value for Δ/Δ when g(x) = g(a). Intuitively, I feel that there's something wrong with statement (ii), but I can't place a finger on precisely what's wrong with it.
Edit: Sorry, I meant to post this as a response to another comment, not as an answer. I am new to the website.