What Does "Tangent to a Point on a Curve" Mean?

Question

Is has been stated in an earlier answer to another question that a "point" is an undefined concept in mathematics.

If this is true, how can we define "tangent to a point on a curve"?

Answer 1

Basically, a tangent line through a given point on a curve is the boundary of a half-plane which contains a segment of the curve to either side of the point, and for which the point itself is on the boundary.

I will give you an example:

Say the curve $y = 5 - x^2$ at the point $(1,4)$ on the curve and you want to find the slope of line tangent to a curve at that given point. You would basically utilize the derivative, $$f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$$ to find the slope of the tangent line to the curve at the point $(1, 4)$, where $$y = f(x) = 5 - x^2$$ So, $$\begin{align} f'(x) =\lim_{h \to 0} \frac{f(x + h) - f(x)}{h} & = \lim_{h \to 0} \frac{\Big(5 - (x + h)^2\Big) - (5 - x^2)}{h} \\ \\ & = \lim_{h\to 0}\frac{5 - (x^2 + 2hx + h^2) - 5 + x^2}{h} \\ \\ & = \lim_{h\to 0}\frac {-2hx - h^2}{h} \\ \\ & = \lim_{h\to 0}\frac{-h(2x + h)}{h} \\ \\ & = \lim_{h\to 0} -(2x + h)\\ \\ f'(x) & = -2x \end{align}$$

Now, at $(1, 4), \;x = 1$, so the slope at that point is given by $f'(1) = -2(1) = -2$.

Here is a depiction of how Wolfram Alpha shows it: (Image compliments of WolframAlpha).

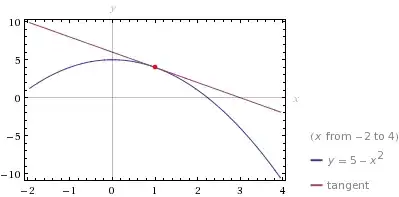
If you want to go further and find the actual equation of the line then, you can find the equation line tangent to $y = 5-x^2$ at the point $(1,4)$ knowing the slope of the line is $-2$, and the fact that $(1, 4)$ lies on that line. We know the equation of a line can be written in the form $(y - y_0) = m(x - x_0)$, where $m$ represents the slope of the line, and $(x_0, y_0)$ represents a point on the line.

In our case, we've found slope to be given by $-2$, and $(x_0, y_0) = (1, 4)$. So, $$y - 4 = -2(x - 1) \iff y - 4 = -2x + 2 \iff y = 6 - 2x$$