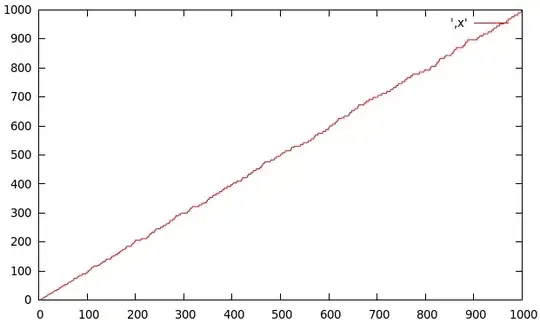
I computed the LCM for all natural numbers from 1 up to a limit $n$ and plotted the result over $n$. Due to the fast-raising numbers, I plotted the logarithm of the result and was surprised to find a (more or less) identity curve ($x=y$).
In other words, $LCM(1, 2, 3, ..., n)$ appears to be roughly the value $e^n$.
Is a there a simple explanation on why this is so?
$LCM(a, b, c, …)$ shall be defined as the least common multiple of all arguments $a, b, c, …$