A equation of Trigonometry

Question

hello dear friends please help me to solve this problem.Thanks very much. How much are $a$ and $b$ in the problem below?

$$1-2\cos 3a +2\cos 3b=0$$$$1-2\cos 5a +2\cos 5b=0$$

Answer 1

The main difficulty in solving those equations is the two different ways of using each variable, such as $a$ in $\cos 3a$ and $\cos 5a$. One way to remove that problem is to express each of those in terms of the same expression. If you use the cosine and sine addition identities and let $x=\cos a$ you will get

$$\cos 3a=4x^3-3x$$ $$\cos 5a=16x^5-20x^3+5x$$

Do similarly for $y=\cos b$ and substitute and you will get two equations in $x$ and $y$ which are now directly comparable. Even though you now have fifth powers and the like this may easier for you than the original equations.

Answer 2

Just add the equations , take 2 common and use this formula cos3a + cos5a = 2cos4acosa similarly for cos3b and cos5b.. Try to solve further May this help...

Answer 3

The following Mathematica code returns the solution to your problem and it involves roots of 12th degree polynomials combined with the arcus tangens function (if you can't access Mathematica, here is the output: (click).

Solve[1-2Cos[3a]+2Cos[3b]==0 && 1-2Cos[5a]+2Cos[5b]==0, {a,b}]

Answer 4

Some partial result. Subtracting equation $(1)$ from equation $(2)$ yields $$-2(\cos5a-\cos3a)+2(\cos5b-\cos3b)=0\Rightarrow \cos5a-\cos3a=\cos5b-\cos3b$$ Using subtraction formulae for the cosine we get $$\sin\Big(\frac{5a+3a}{2}\Big)\sin\Big(\frac{5a-3a}{2}\Big)=\sin\Big(\frac{5b+3b}{2}\Big)\sin\Big(\frac{5b-3b}{2}\Big)\Rightarrow \sin4a\sin a=\sin4b\sin b$$ Adding equation $(1)$ to equation $(2)$ yields $$2-2(\cos5a+\cos3a)+2(\cos5b+\cos3b)=0$$ Using the summation formulae for cosine we get $$1-2\cos4a\cos a+2\cos4b\cos b=0$$ So the problem is equivalent to find the solution of the following system \begin{cases}\sin4a\sin a-\sin4b\sin b=0\\1-2\cos4a\cos a+2\cos4b\cos b=0\end{cases} First of all there is no solution of the form $a=b$ as the second equality would not hold. Second neither $a$ nor $b$ can be zero. Assume $a=0$ then from the first equation we must have $b=\pi n$ or $b=\frac{\pi n}{4}$ for $n\in\mathbb{Z}$. However from the second equation one would get $$1-2\cdot1\cdot1+2\cos(4\pi n)\cos(\pi n)=0\Rightarrow1\cdot2\cdot(-1)^n=1$$ or $$1-2\cdot1\cdot1+2\cos(4\frac{\pi n}{4})\cos(\frac{\pi n}{4})=0\Rightarrow\cos(\frac{\pi n}{4})=\frac{(-1)^{n}}{2}$$ But clearly neither of the results above can hold true. So we have $a\neq b$ and $a,b\neq0$.

Answer 5

It is sufficient to find the solutions $(a,b)$ in the square $[0,\pi]^2$. In the following figure (obtained by joining two Mathematica contour plots) the large red ovals show the points $(a,b)$ satisfying the first equation, and the small blue ovals show the points satisfying the second equation. One can surmise that the global situation created by these two equations is very intricate indeed. I can distinguish five different kinds of solution points not equivalent under symmetries.

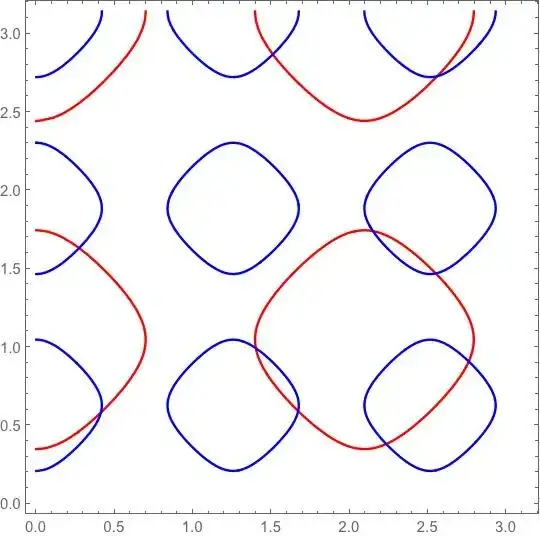
In order to find the solutions numerically use the figure for starting estimates $(a_0,b_0)$ and then proceed, e.g,. by means of the Newton-Raphson method.