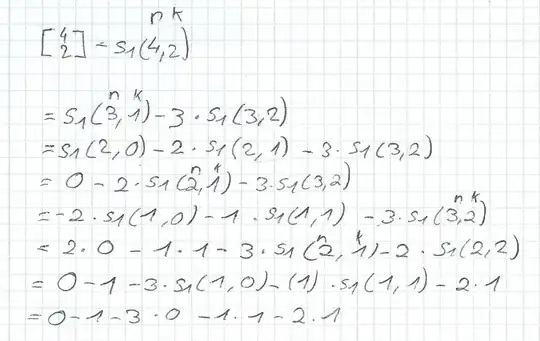2

I am trying to calculate the stirling numbers of the first kind. I am not very good in math and there is not a single example somewhere in the internet. So I would really appreciate it if you could help me there.

The stirling number which I want to calculate is s1(4,2). I know the solution is 11. How far I came: enter image description here

user3333587
  • 33

1 Answers1

2

You could use the rising factorial to find $\left[\begin{array}{c} 4 \\ 2 \end{array}\right]$. It goes as follows:

$$(x)^4 = x(x+1)(x+2)(x+3) = x^4 + 6x^3 + 11x^2 + 6x$$

$\left[\begin{array}{c} 4 \\ k \end{array}\right]$ is now the coefficient with $x^k$. Thus $\left[\begin{array}{c} 4 \\ 2 \end{array}\right]$ = 11.

For the recurrence relation with the unsigned Stirling numbers of the first kind, you would have:

$$\begin{align} \left[\begin{array}{c} 4 \\ 2 \end{array}\right] & = 3\left[\begin{array}{c} 3 \\ 2 \end{array}\right] + \left[\begin{array}{c} 3 \\ 1 \end{array}\right]\\ & = 3\left(2\left[\begin{array}{c} 2 \\ 2 \end{array}\right] + \left[\begin{array}{c} 2 \\ 1 \end{array}\right]\right) + 2\left[\begin{array}{c} 2 \\ 1 \end{array}\right] + \left[\begin{array}{c} 2 \\ 0 \end{array}\right] = 6\left[\begin{array}{c} 2 \\ 2 \end{array}\right] + 5\left[\begin{array}{c} 2 \\ 1 \end{array}\right] + 0 \\ & = 6\left(\left[\begin{array}{c} 1 \\ 2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 1 \end{array}\right]\right) + 5\left(\left[\begin{array}{c} 1 \\ 1 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right]\right) = 6\left[\begin{array}{c} 1 \\ 2 \end{array}\right] + 11\left[\begin{array}{c} 1 \\ 1 \end{array}\right] + 0 \\ & = 6\left(0 + \left[\begin{array}{c} 0 \\ 1 \end{array}\right]\right) + 11\left(0\left[\begin{array}{c} 0 \\ 1 \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \end{array}\right]\right) = 11 \end{align}$$

For the recurrence relation with the signed Stirling numbers of the first kind, you would get:

$$\begin{align} \mathrm{s}(4,2) & = -3 \mathrm{s}(3,2) + \mathrm{s}(3,1) \\ & = -3[-2\mathrm{s}(2,2) + \mathrm{s}(2,1)] -2\mathrm{s}(2,1) + \mathrm{s}(2,0) = 6\mathrm{s}(2,2) -5\mathrm{s}(2,1) + 0 \\ & = 6[-\mathrm{s}(1,2) + \mathrm{s}(1,1)] -5[-\mathrm{s}(1,1) + \mathrm{s}(1,0)] = -6\mathrm{s}(1,2) + 11\mathrm{s}(1,1) - 0 \\ & = -6[0 + \mathrm{s}(0,1)] + 11[0 + \mathrm{s}(0,0)] = 11 \end{align}$$

Mr Tsjolder from codidact
  • 814
  • Ok thanks for your answer. But if I can calculate the amount of permutations in partitions with the rising factorial why are there stirling numbers of the first kind? – user3333587 Jan 16 '15 at 08:32
  • I'm not a real mathematician, but I think it's just a name for the numbers. It's like asking what the sense of defining a Dedekind number is... (my guess...) You should note though that the recurrence relation is more practical for big n or to write algorithms with. – Mr Tsjolder from codidact Jan 16 '15 at 13:05