Why ternary diagrams work

Question

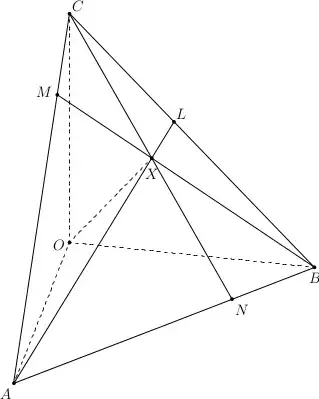
I am trying to understand why ternary diagrams work. In order that the altitude criterion be valid, if I correctly understand, given equilateral triangle $ABC$, whose vertices I name as the three phases $A,B,C$, the sum $XL'+XM'+XN'$ (see figure on the left; I use the same notation for sides and their length) of the distances of point $X$, contained inside the triangle, from the sides must equate the height of $ABC$. Why does that holds?

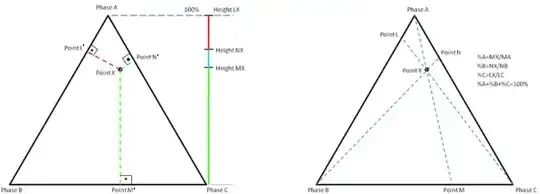
Moreover, in order that the intersection method hold and the ratios between the three phases be respected, I would say that, if we respectively call $L,M$ and $N$ the intersection point between straight line $\overline{CX}$ and $AB$, between straight line $\overline{AX}$ and side $BC$ and between straight line $\overline{BX}$ and side $AC$, I would say that the following equality should hold:$$\frac{AN}{CN}=\frac{AL}{BL}\frac{BM}{CM}$$because, if $a,b$ and $c$ respectively are the quantities of phases $A,B$ and $C$, I would say that the equality is equivalent to $\frac{c}{a}=\frac{b}{a}\frac{c}{b}$ (where the factors correspond to each other: $\frac{c}{a}=\frac{AN}{CN}$ etc.). How can it be proved?

While ternary diagrams are ubiquitous in several sciences, like geology, I can find nothing explaining the mathematical foundations of such diagrams, why they work. I suspect that what I have said can be proved by using elementary or analytic geometry, but I must admit that I can find no way to prove them to myself (there is possibly some rust on my knowledge of elementary geometry). I thank you very much for any answer!

Answer 1

The diagram below uses a slightly different labeling ($A$, $B$, and $C$ are opposite $L$, $M$, and $N$ respectively). Here's a computational justification of the intersection method. (It's possible there are simpler arguments.)

Let $(x, y, z)$ denote spatial Cartesian coordinates. Without loss of generality, the triangle lies in the plane with equation $x + y + z = 1$. If $X = (a, b, c)$, then the labeled points have Cartesian coordinates \begin{align*} A &= (1, 0, 0), & B &= (0, 1, 0), & C &= (0, 0, 1), \\ L &= \frac{1}{b + c}(0, b, c),& M &= \frac{1}{a + c}(a, 0, c),& N &= \frac{1}{a + b}(a, b, 0). \end{align*} By the Cartesian distance formula, $$ XA^{2} = (1 - a)^{2} + b^{2} + c^{2} = (b + c)^{2} + b^{2} + c^{2} = 2(b^{2} + bc + c^{2}) $$ and $$ LA^{2} = 1 + \frac{b^{2} + c^{2}}{(b + c)^{2}} = 2\frac{b^{2} + bc + c^{2}}{(b + c)^{2}}. $$ Thus $\dfrac{XA}{LA} = b + c = 1 - a$. By similar calculations (or symmetry of the labels!), $\dfrac{XB}{MB} = a + c = 1 - b$ and $\dfrac{XC}{NC} = a + b = 1 - c$.

It follows that $$ \frac{LX}{LA} = 1 - \frac{XA}{LA} = a,\quad \frac{MX}{MB} = b,\quad \frac{NX}{NC} = c, $$ so that $\dfrac{LX}{LA} + \dfrac{MX}{MB} + \dfrac{NX}{NC} = a + b + c = 1$, as claimed.