I learned this formula for the Fibonacci series, and its respective proof in one of my Computer Science classes.
F(0) = 0; F(1) = 1; F(2) = 1
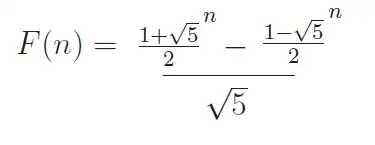 However, I am taking an abstract mathematics class and this slightly different formula has taken me nowhere for the past 2 hours...
However, I am taking an abstract mathematics class and this slightly different formula has taken me nowhere for the past 2 hours...

I end up getting $3 + \sqrt 5 / 1 + \sqrt 5$ and $ 3 - \sqrt 5 / 1 - \sqrt 5$ in a part where I should get $1 + \sqrt 5 /2$ and $ 1 - \sqrt 5 /2$ to generate the formula in terms of n+1 by complete induction.
I noticed one of the differences is the boundaries, one starts with F(0) = 1, the other one with F(0) = 0.
The first one is easily proven in 6 lines...
The second one gives me these weird values that I can't reduce.
Can someone explain to me how to approach this?