I need to find a group homomorphism from $SL_2 (\mathbb Z / 5 \mathbb Z)$ to $S_5$. There is obviously the trivial homomorphism but I am then asked to deduce that $SL_2 (\mathbb Z / 5 \mathbb Z)/\{I,-I\} \cong A_5$, so ideally I want a homomorphism with kernel $\{I,-I\}$, and image $A_5$ so I can use the isomorphism theorem. Any hints?
-
1You could show that ${\rm PSL}(2,5)$ is a simple group of order $60$, and use thus that $A_5$ is the unique simple group of order $60$. You can show more generally that ${\rm PSL}(2,K)$ is simple provided $K$ has more than three elements. – Pedro Jan 12 '15 at 23:14
-
As a general tactic, morphisms $G\to S_n$ arise whenever $G$ has a subgroup of index $n$, see this. If you could show that ${\rm SL}(2,5)$ has a subgroup of index $5$ that contains the center of ${\rm SL}(2,5)$ you might be in good path. – Pedro Jan 12 '15 at 23:41
-
(It is interesting to note that ${\rm SL}(2,5)$ is not isomorphic to $S_5$, however!) – Pedro Jan 12 '15 at 23:48
-
This is related to http://math.stackexchange.com/questions/1096446 – Derek Holt Jan 13 '15 at 09:19
-
2@PedroTamaroff Yes, there are three non-solvable groups of order $120$, $S_5$ with a $2$ at the top, ${\rm SL}(2,5)$ with a $2$ at the bottom, and $A_5 \times C_2$ with both. – Derek Holt Jan 13 '15 at 09:21
2 Answers
I couldn't claim that this is an easiest way; but I have explained once this solutionway in my classroom for undergraduates.
The group $A_5$ has presentation $\langle x,y\colon x^2=1, y^3=1, (xy)^5=1\rangle$.
We can obtain a homomorphism you expect by this presentation. We find a pair of elements $X,Y$ in $SL(2,5)$ such that $X$ has order $2$, $Y$ has order $3$ and $(XY)$ has order $5$.
Each element of $SL(2,5)$ gives a Mobius transformation $z\mapsto \frac{az+b}{cz+d}$ where $a,b,c,d$ are in the domain=codomain=$\{0,1,2,3, 4,\infty\}$ of the transformation (convention $1/0=\infty$ and $1/\infty=0$). So we may try to find two Mobius transformation, one of order $2$, one of order $3$ so that their product has order $5$.
One choice for Mobius map of order $2$ is $z\mapsto \frac{-1}{z}$. For order $3$ Mobius map, one possibility is to find a map $z\mapsto \frac{az+b}{cz+d}$, such that $0\mapsto 1\mapsto \infty\mapsto 0$ (so that its order will be $3$), and it is in fact $z\mapsto \frac{1}{1-z}$.
Now it is easy to check that their product turns out to be order $5$.
What are the corresponding element in $SL(2,5)$? Well. These are $$X= \begin{bmatrix} 0 & 1\\ -1 & 0\end{bmatrix} \mbox{ and } Y= \begin{bmatrix} 1 & 0\\ -1 & 1 \end{bmatrix}$$ which can be written just by considering the coefficients involved in the Mobius transformations. Now, the map $X\mapsto x$ and $Y\mapsto y$ can be uniquely extended to a homomorphism $f\colon SL(2,5)$ to $A_5$ (or $S_5$) (from the definition of the free group; I will not make it too technical.) And, thats it. .
- 10,238
-
You said that you were looking for $X$ and $Y$ in ${\rm SL}(2,5)$ such that $X$, $Y$, and $XY$ have orders $2,3,5$, but in your final choice of $X$ and $Y$, they have orders $4,5,3$. Note also that the only element of ${\rm SL}(2,5)$ of order $2$ is $-I_2$, which is in its centre. – Derek Holt Jan 13 '15 at 13:17
-
Yaa! If we go modulo ${\pm I}$, then we get a homomorphism. So here $SL(2,5)\rightarrow PSL(2,5)\rightarrow A_5$ is the required homomorphism, where first one is quotient and second is obtained by $\bar{X}\mapsto x$, $\bar{Y}\mapsto y$. Thanks for notification. – Groups Jan 13 '15 at 15:23
Just wanted to add some extra commentary.
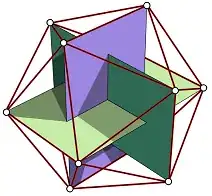
Let $I$ be the rotational symmetry group of the (regular) icosahedron. By orbit-stabilizer, it has order $60$. It is a subgroup of $\mathrm{SO}(3)$, the full group of $3\times3$ rotation matrices. Every edge of the icosahedron uniquely determines a compound of three inscribed semiperpendicular golden rectangles:
There are $6$ icosahedron edges per compound, so there are $30/6=5$ compounds. Note $I$ acts on this set $\Omega$ of $5$ compounds, indeed we may identify $I$ with an index $2$ subgroup of $\mathrm{Sym}\,\Omega$, forcing it to be the alternating subgroup by uniqueness. Thus, $I\cong A_5$ by labelling the compounds $1$ thru $5$.
On the other hand, there is a double cover $2I$ of the icosahedral group (called the binary icosahedral group), which is the preimage of $I$ under the $2$-to-$1$ group homomorphism $S^3\to\mathrm{SO}(3)$, where $S^3$ is the group of versors (unit quaternions). (There are many resources discussing how the antipodal versors $\pm \exp(\theta\mathbf{u})$ represent the $3$D rotation around the $\mathbf{u}$-axis by $2\theta$, where $\mathbf{u}$ is a unit vector.) By considering quaternions as a $2$D complex vector space, we may identify quaternions with $2\times2$ complex matrices, in which case $S^3$ may be identified with $\mathrm{SU}(2)$. Then the elements of $2I$ may be reduced mod $5$ to get $\overline{2I}=\mathrm{SL}_2(\mathbb{F}_5)$. Since the kernel of $2I\to I$ corresponds to the kernel of $\mathrm{SL}_2(\mathbb{F}_5)\to\mathrm{PSL}_2(\mathbb{F}_5)$, we conclude $I\cong\mathrm{PSL}_2(\mathbb{F}_5)$.
Thus, $\mathrm{PSL}_2(\mathbb{F}_5)\cong A_5$. I explained this in my answer here.
Symmetric groups have trivial outer automorphism group, except for the exceptional case of $\mathrm{Out}\,S_6=\mathbb{Z}_2$. An outer automorphism of $S_6$ swaps cycle types $(\cdot\cdot)$ and $(\cdot\cdot)(\cdot\cdot)(\cdot\cdot)$ as well as $(\cdot\cdot\cdot)$ with $(\cdot\cdot\cdot)(\cdot\cdot\cdot)$. While the subgroup $A_5$ stabilizes a point, its image under an outer automorphism is an "exotic" copy of $A_5$ which is actually transitive. This matches (up to relabelling) the action of $\mathrm{PSL}_2(\mathbb{F}_5)$ on $\mathbb{F}_5\mathbb{P}^1$ and of $I$ on the set $\Phi$ of antipodal pairs of vertices of the icosahedron (note $|\mathbb{F}_5\mathbb{P}^1|=|\Phi|=6$ in contrast to $|\Omega|=5$).
- 151,657