I tried doing this with regular method and computations became very complex .Is there any shorter way , Am i missing something ?
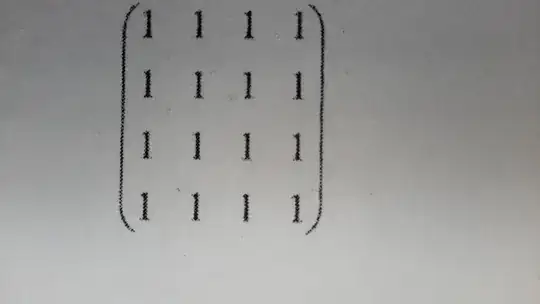
I tried doing this with regular method and computations became very complex .Is there any shorter way , Am i missing something ?

Hint: Since all columns (or alternatively all rows) all equal, the rank of the matrix is 1
It can be done by using the characteristic equation:
Let us assume that the characteristic equaton of the matrix A is:
$$ \lambda^4 + a_1\lambda^3 + a_2\lambda^2 + a_3 \lambda + a_4 = 0$$
If you check then,
$$A^2 = 4 A$$
Using the fact that a matrix satisfies its own characteristic equation we get:
$$A^4 = 4 A^3 $$
Again writing it in terms of the Eigen values we get:
$$ \lambda^4 - 4 \lambda^3 = 0$$
Solve this and you will get two distinct Eigen values: 4 and 0.