In financial mathematics, you're looking at a problem of compound interest rates (over $\mathbf{n}$ compoundment periods), where $100x$ is the percentage interest rate or yield and $\mathbf{x}$ the relative accrual rate per period. When $n$ is the number of compoundment periods per year, $\mathbf{nx}$ is the nominal annual interest rate and $\mathbf{f(x)}$ is a unitless quantity comparing the growth over $\mathbf{n}$ periods with the growth over just one period, and is applicable for example on a fixed-rate mortgage when $n=12$. In this context, $\mathbf{x \cdot f(x)}$ is the equivalent yearly rate, also known as annual percentage rate (APR), annual equivalent rate (AER), and other various combinations of
$$
\text{annual/-}
\quad
\text{effective/equivalent/-}
\quad
\text{interest/percentage/-}
\quad
\text{rate/yield}
$$
(i.e. about 42 different wordings if we require at least one of the words 'annual', 'effective' or 'equivalent' -- to be clear what we're talking about --- but allow their order to be interchanged if using two).
Usually, the problem you are given does not have the $x$ in the denominator, making the problem easily solvable with logarithms and a ratio of future and present values. Most financial calculators have a way to solve this directly. There are surely good web resources as well. Once could program this in Javascript for use offline; someone probably already has.
Without such a resource, or if programming it yourself, here's what you'd need (and don't need) to know about $f(x)$.
First some of the many alternate algebraic forms
(for $x\in\mathbb{R}$ and $n\in\mathbb{Z}$ both positive):
$$
\eqalign{
f(x)
&=\frac{(1+x)^n-1}{x}
=\sum_{k=1}^n
\binom{n}{k}
x^{k-1}
}
$$
and factorizations (also perhaps of interest to math majors):
$$
\eqalign{
f(x)
&=\frac{(1+x)^n-1}{(1+x)-1}
=\prod_{k=1}^{n-1}
\left(x+1-
e^{\frac{2\pi ik}{n}}
\right)
=\prod_{1<d|n}
\Phi_d
\left(x+1\right)
\cr
&=\left(x+2\right)^{
\left\lfloor\frac{ n }2\right\rfloor
-\left\lfloor\frac{n-1}2\right\rfloor}
\prod_{k=1}^{
\left\lfloor\frac{n-1}2\right\rfloor}
\left(x^2+\left(2\sin\tfrac{k\pi}{n}\right)^2(x+1)\right)
\cr
}
$$
The first line gives the same form you gave as the starting point for this problem, i.e. the relative growth from $n$ compounding periods compared with the growth from one period. The second formula gives an expression for $f(x)$ as a monic polynomial of degree $n-1$, with the multipliers of the various powers of $x$ known as binomial coefficients.
The second line gives some alternate representations which are quite meaningful in the complex plane and in elementary number theory. These equations say that the roots of the polynomial $f(x)$ lie on a unit circle centered at $-1$ and are equally spaced to form a regular $n$-gon, with the exception of the removed root at $x=0$ in the denominator on the LHS. Each root $e^{\frac{2\pi ik}{n}}-1$ makes an angle of $\frac{2\pi ik}{n}$ with the positive real axis as it extends radially from $-1$. The formula on the RHS says that these roots can be grouped by the denominator of $\frac{k}{n}$ in lowest terms.
The third line performs a different grouping, into quadratic factors corresponding to pairs of complex conjugate roots, except for a linear factor $x+2$ for the root at $-2$ in case $n$ is even; this last optional bit is performed with the expression
$\left\lfloor\frac{ n }2\right\rfloor
-\left\lfloor\frac{n-1}2\right\rfloor
=(n-1)-
2\left\lfloor\frac{n-1}2\right\rfloor$,
which gives the remainder of $n-1$ modulo $2$, i.e. it is $0$ or $1$ depending on whether $n$ is odd or even. All coefficients here are again real, and all factors are irreducible over real fields.
An interesting consequence of this, looking at $f(0)$, is that
$$
\prod_{k=1}^{\left\lfloor\frac{n-1}2\right\rfloor}
\sin^2\tfrac{k\pi}{n}
=\frac{n}{2^{n-1}}.
$$
Next, $f$ is increasing for $x>0$ and $n>1$,
as can be seen from its derivative:
$$
\eqalign{
f\,'(x)
&=\frac{(x+1)^{n-1}\big((n-1)x-1\big)+1}{x^2}
=\sum_{k=2}^n
\binom{n}{k}
(k-1)x^{k-2}
}
$$
Extra notes:
- $f(x)<\frac{e^{nx}-1}{x}$ for $x>-1$. Both sides approach $n$ as $x \rightarrow 0$. The inequality actually holds for all $x>-1$ and is strict for $x\ne0$. This follows from observing that $\ln(1+x)$ is increasing and convex with tangent line $y=x$ at the origin.
- Defining $f(0)=n$ (or taking the binomial power sum as our definition) would make $f$ continuous at $0$, extending the domain to $(-1,\infty)$, since $f(x)$ approaches the derivative of the power function with power $n$ as $x \rightarrow 0$.
- For $n=1$, $f(x)$ is also $1$.
- $\frac{x}{n}f(\frac{x}{n}) \rightarrow e^x-1$ as $n \rightarrow \infty$.
- With $f(0)=0$, the derivative $f\,'(0)=\frac{n(n-1)}{2}$ exists and is continuous.
- $f\,'(x)=1$ for $n=2$.
- Solving $y=f(x)$ for $x$ given $y$ will have one solution for $y>n$ ($y\ge n$ if we allow $x=0$), and no solutions for $y<n$. There are a host of methods for rootfinding, and some specialized ones for polynomials. Newton's method, the simpler bisection method, a combination of bisection and secant resulting in a simplified version of Brent's method (as @JM pointed out), or a matrix method such as @NickAlger mentions could be used to find $x$. For Newton-s method, you would use the target function $F(x)=f(x)-y$, and a starting value such as
$$x_0=\frac3{2n}\left(\sqrt{1+\frac83\left(\frac{y}{n}-1\right)}-1\right)$$
to iteratively find the root of $F$ by repeatedly setting $x_{n+1}=x_n+\Delta x_n$ for
$$
-\Delta x_n=\frac{F(x)}{F\,'(x)}=\frac{f(x)-y}{f\,'(x)}=
\frac{x\left[(1+x)^n-(1+xy)\right]}{1-(1+x)^{n-1}\left[1-(n-1)x\right]}
$$
(where I have omitted the $n$ subscript after each $x$ and
encapsulated the negative sign of $\Delta x_n$ on the LHS for brevity).
This may seem more complicated than bisection, but convergence is much more rapid, meaning fewer iterations are needed to get a precise answer. (The value of $x_0$ above comes from using the upper bound $\frac{e^{nx}-1}{x}$ as an estimate for $f(x)$, expanding $e^{nx}$ in a Taylor series, simplifying, and using the quadratic equation on the lowest remaining terms.)
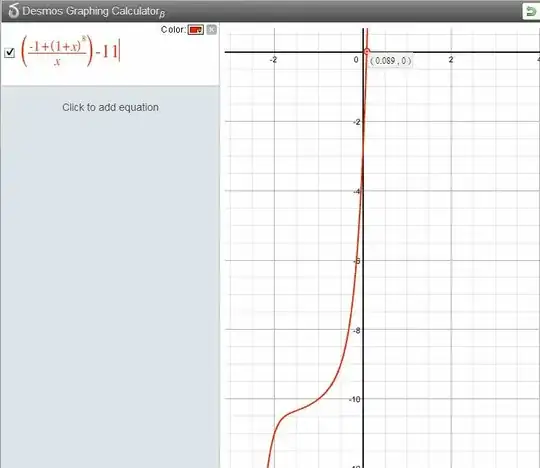
Finally, in your problem, $n=8$, so $f(x)=y=11>8$ has solution $x \approx 0.08928634$, or $8.93$%.
Here is an example solution using Newton's method and sage (online), which is correct to about ten places after the third iteration (and to about a hundred after the seventh!):
n = 8
y = 11
F,f,x = var('F,f,x')
f = ((1+x)^n - 1) / x
F = x - x * ((1+x)^n - (1+x*y)) / (1 - (1+x)^(n-1) * (1-(n-1)*x))
x = 3/2/n * (sqrt(1 + 8/3*(y/n - 1)) - 1) # x_0
x = x.n(digits=100)
for i in range(10):
e = (f(x) - y).n(digits=100) # error
print i, x.n(), e.n()
x = (F(x)).n(digits=100) # next estimate
# i x e:
0 0.0776650429449553 -0.452683820096624
1 0.0895542025788610 0.0106779696847534
2 0.0892864798024252 5.56813083089398e-6
3 0.0892863400500602 1.51628362736157e-12
4 0.0892863400500221 1.12440509060997e-25
5 0.0892863400500221 6.18311776700343e-52
6 0.0892863400500221 -1.71448108692341e-99
7 0.0892863400500221 0.000000000000000
8 0.0892863400500221 -2.28597478256455e-100
9 0.0892863400500221 9.14389913025820e-100