Let $W_{t}$ be a brownian motion and $$ W^{*}_{t} = \max_{s<t} W_{s} $$
Then can you please explain why we have this: $$ (W^{*}_{t} - W_{t})dW^{*}_{t} = 0 $$
Let $W_{t}$ be a brownian motion and $$ W^{*}_{t} = \max_{s<t} W_{s} $$
Then can you please explain why we have this: $$ (W^{*}_{t} - W_{t})dW^{*}_{t} = 0 $$
Process $W_t^\ast = \max_{s < t} W_s$ is caglad (left-continuous with the right limit) piecewise constant:
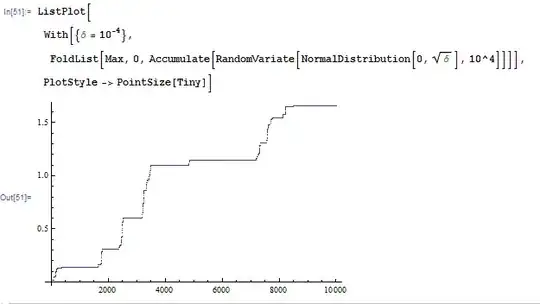
Therefore, intuitively speaking, $\mathrm{d} W_t^\ast$ is mostly zero. At the points of discontinuities of $W_t^\ast$, the Wiener process $W_t$ crosses $W_t^\ast$ from below, meaning that $W_t^\ast = W_t$. Now whether this makes the product $(W_t-W_t^\ast) \mathrm{d} W_t^\ast$ zero depends on details of what you mean by $\mathrm{d}W_t^\ast$, which you did not provide.