The orthocenter of $\triangle ABC$ is $H$. Let $B'$ be a point on AC and $C'$ be a point on AB, such that $BCB'C'$ is a cyclic quadrilateral. Let the orthocenter of $\triangle AB'C'$ be $H'$.
Prove that the lines $BB', CC'$and $HH'$ are concurrent.
I am quite lost on how to solve the question. I know that $\triangle AB'C'$ is similar to $\triangle ABC$, but how may I use this to advantage? Can anyone help? :)
Here's an approach using multiple applications of an Extended Ceva's Theorem that I introduced in a previous answer. The theorem gives a condition for concurrence of (almost) any three lines passing through the edges of a triangle, not just those through vertices.
Extended Ceva's Theorem. Consider points $D_1$, $D_2$, $E_1$, $E_2$, $F_1$, $F_2$ on the (extended) edges of $\triangle ABC$, with each $D_i$, $E_i$, $F_i$ on the (extended) edge opposite vertex $A$, $B$, $C$, respectively.
Lines $\overleftrightarrow{D_1E_2}$, $\overleftrightarrow{E_1F_2}$, $\overleftrightarrow{F_1D_2}$ concur if and only if $$\begin{align} 1 &= \frac{|BD_1|}{|D_1C|} \frac{|CE_1|}{|E_1A|} \frac{|AF_1|}{|F_1B|} + \frac{|D_2C|}{|BD_2|} \frac{|E_2A|}{|CE_2|} \frac{|F_2B|}{|AF_2|} \\[6pt] &+ \frac{|BD_1|}{|D_1C|} \frac{|D_2C|}{|BD_2|} + \frac{|CE_1|}{|E_1A|} \frac{|E_2A|}{|CE_2|} + \frac{|AF_1|}{|F_1B|} \frac{|F_2B|}{|AF_2|} \qquad (\star) \end{align}$$
In the current scenario, we could take our lines to be $\overleftrightarrow{BB^\prime}$, $\overleftrightarrow{CC^\prime}$, and $\overleftrightarrow{HH^\prime}$. The last of these we would need to extend to give points, say $D$ on $\overleftrightarrow{BC}$ and $E$ on $\overleftrightarrow{CA}$.
The corresponding concurrence condition arises from the substitutions $$F_2 \to B, \quad E_1 \to B^\prime, \quad D_2 \to C, \quad F_1 \to C^\prime, \quad D_1 \to D, \quad E_2 \to E$$ which reduce $(\star)$ to $$\begin{align} 1 &= \frac{|CB^\prime|}{|B^\prime A|}\;\left(\; \frac{|BD|}{|DC|} \frac{|AC^\prime|}{|C^\prime B|} + \frac{|EA|}{|CE|}\;\right) \qquad (1) \end{align}$$
As OP notes, $\triangle AB^\prime C^\prime \sim \triangle ACB$, say with proportionality factor $k$. This makes computing two of the ratios easy:
$$\frac{|CB^\prime|}{|B^\prime A|} = \frac{b - k c }{k c} \qquad\qquad \frac{|AC^\prime|}{|C^\prime B|} = \frac{k b}{c-k b}$$
The remaining two ratios, which we'll name $$ m := \frac{|BD|}{|DC|} \qquad\qquad n := \frac{|EA|}{|CE|}$$ are a little trickier to deduce. One can use coordinates, but for less effort than it takes to determine points $D$ and $E$ from $\overleftrightarrow{HH^\prime}$ and calculate the ratios, you could just verify that the intersection of $\overleftrightarrow{BB^\prime}$ and $\overleftrightarrow{CC^\prime}$ lies on $\overleftrightarrow{HH^\prime}$. There may also be a clever geometric argument leveraging various similar triangles, but I want to try something different.
Instead, we'll take advantage of the fact that each of $H$ and $H^\prime$ is a point of concurrence of $\overleftrightarrow{HH^\prime}$ with two other lines. This gives us two instances of $(\star)$ involving $m$ and $n$, so that we can solve for these values.
First, $H$ is where $\overleftrightarrow{HH^\prime}$ meets $\overleftrightarrow{BP}$ and $\overleftrightarrow{CQ}$. The Extended Ceva's Theorem with the substitutions $$F_2 \to B, \quad E_1 \to P, \quad D_2 \to C, \quad F_1 \to Q, \quad D_1 \to D, \quad E_2 \to E$$ gives $$1 = \frac{|CP|}{|PA|}\;\left(\; m \; \frac{|AQ|}{|QB|} + n\;\right)$$ so that $$1 = \frac{a\cos C}{c\cos A}\;\left(\; m \; \frac{b \cos A}{a \cos B} + n\;\right) = m \; \frac{b \cos C}{c\cos B} + n\;\frac{a \cos C}{c \cos A} \qquad(2)$$
On the other hand, $H^\prime$ is the point where $\overleftrightarrow{HH^\prime}$ meets $\overleftrightarrow{B^\prime P^\prime}$ and $\overleftrightarrow{C^\prime Q^\prime}$. Unfortunately, we can't just make substitutions into $(\star)$ using $B^\prime$, $C^\prime$, $P^\prime$, $Q^\prime$, $D$, $E$, since these points aren't in the appropriate configuration on the edges of $\triangle ABC$. To remedy this, take $X = \overleftrightarrow{BC}\cap\overleftrightarrow{B^\prime P^\prime}$ ; then we can make these substitutions: $$D_2 \to X, \quad F_1 \to P^\prime, \quad F_2 \to C^\prime, \quad E_1 \to Q^\prime, \quad D_1 \to D, \quad E_2 \to E$$ to get $$\begin{align} 1 &= m\; \frac{|CQ^\prime|}{|Q^\prime A|} \frac{|AP^\prime|}{|P^\prime B|} + n \; \frac{|XC|}{|BX|} \frac{|C^\prime B|}{|AC^\prime|} \\[6pt] &+ m\; \frac{|XC|}{|BX|} + n \; \frac{|CQ^\prime|}{|Q^\prime A|} + \frac{|AP^\prime|}{|P^\prime B|} \frac{|C^\prime B|}{|AC^\prime|} \end{align}$$ so that $$\begin{align} 1 &= m\; \frac{b-kb\cos A}{k b \cos A} \frac{k c \cos A}{c - k c \cos A} - n \; \frac{(c-kc\cos A)/\cos B - a}{(c-kc\cos A)/\cos B} \frac{c - k b}{k b} \\[6pt] &- m\; \frac{(c-kc\cos A)/\cos B - a}{(c-kc\cos A)/\cos B} + n \; \frac{b - k b \cos A}{k b \cos A} + \frac{k c \cos A}{c - k c \cos A} \frac{c - k b}{k b} \end{align}$$
(Note the sign change with the $|XC|/|BX|$ terms, since $\overrightarrow{XC}$ and $\overrightarrow{BX}$ point in opposite directions.) This becomes
$$ k c \cos A \cos C = m\;k b \cos A\cos B + n \; ( c \sin A \sin B - k \cos A ( c \cos C + b \cos B )) \quad (3)$$
Solving $(2)$ and $(3)$ for $m$ and $n$ gives $$ m = \frac{(c - k b ) \cos B}{(b - k c ) \cos C} \qquad\qquad n = \frac{k (b^2-c^2) \cos A}{a ( b - k c )\cos C} $$ and one can verify that these satisfy $(1)$, proving the concurrence of $\overleftrightarrow{BB^\prime}$, $\overleftrightarrow{CC^\prime}$, $\overleftrightarrow{HH^\prime}$. $\square$
Admittedly, the algebraic details got a bit hairier than I intended when I embarked on this journey. (The reader is invited to derive $m$ and $n$ via clever geometry, so as to use $(1)$ more-directly.) Nevertheless, I think this makes for a not-unreasonable application of the Extended Ceva Theorem.
Here is a complete proof along the lines of my comments to the OP. Most of it is well-known stuff, but it probably doesn't hurt to build it from scratch.
First of all, the problem follows from the following claim:
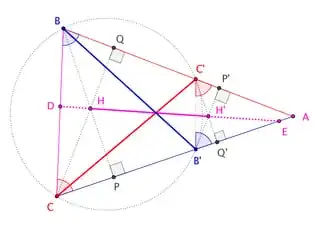
Theorem 1. Let $A$, $B$, $C$ and $D$ be four points on a circle. Let $X=AB\cap CD$ and $Y=BC\cap DA$. (I use the notation $\ell\cap m$ to denote the point of intersection of two lines $\ell$ and $m$, even though it would be more formally correct to say that $\ell\cap m$ is a one-element set consisting of this point. I also pretend that everything is in general position when needed, as usually done in this kind of geometry.) Then, the orthocenters of the triangles $XBC$, $XDA$, $YAB$ and $YCD$ lie on one line, and the point $AC\cap BD$ also lies on this line.
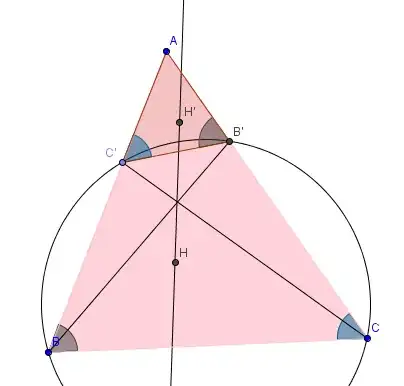
To recover the original problem from this theorem, we need to apply it to $C$, $B^{\prime}$, $C^{\prime}$, $B$ and $A$ instead of $A$, $B$, $C$, $D$ and $X$.
Theorem 1 is not the pinnacle of generality. Indeed, there is a more well-known fact which generalizes it:
Theorem 2. Let $A$, $B$, $C$ and $D$ be four points on the plane. Let $X=AB\cap CD$ and $Y=BC\cap DA$. Then:
(a) The midpoints of the segments $AC$, $BD$ and $XY$ lie on one line.
(b) The circles with diameters $AC$, $BD$ and $XY$ are coaxal (i.e., their pairwise radical axes coincide).
(c) The orthocenters of the triangles $XBC$, $XDA$, $YAB$ and $YCD$ all lie on the radical axis of any two of the circles with diameters $AC$, $BD$ and $XY$.
(d) If the points $A$, $B$, $C$ and $D$ lie on one circle, then the point $AC\cap BD$ also lies on this radical axis.
It is clear that parts (c) and (d) of Theorem 2, when combined, yield Theorem 1. It therefore only remains to prove Theorem 2.
Part of Theorem 2 (I am not sure which part) is called the Gauss-Bodenmiller theorem. Also, the line constructed in Theorem 2 (a) is known as the Gauss-Newton line of the complete quadrilateral formed by the lines $AB$, $BC$, $CD$ and $DA$. The radical axis in Theorem 2 (c) is known as the Miquel-Steiner line of this complete quadrilateral. Notice that Theorem 2 (a) is a purely affine statement (i.e., it involves only constructions invariant under affine transformations, such as midpoints of segments and intersections of lines), but we will prove it as a side effect of an argument that involves circles.
Proof of Theorem 2. We introduce the notation $\operatorname*{Thal} \left( PQ\right) $ for the circle with diameter $PQ$, where $P$ and $Q$ are any two points. We also define $\operatorname*{Rad}\left( k,k^{\prime }\right) $ to be the radical axis of two circles $k$ and $k^{\prime}$. Finally, we let $H_{PQR}$ denote the orthocenter of any triangle $PQR$.
We notice that the orthocenters $H_{XBC}$, $H_{XDA}$, $H_{YAB}$ and $H_{YCD}$ are pairwise distinct when $A$, $B$, $C$ and $D$ are in general position. This allows us to WLOG assume that these four orthocenters are distinct; we will use this assumption below.
Let us begin by proving that $H_{XBC}\in\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $. Indeed, let $B^{\prime}$ be the foot of the altitude of triangle $XBC$ emanating from $B$. Then, $H_{XBC}\in BB^{\prime}$, so that $BB^{\prime }=BH_{XBC}$. Also, $BB^{\prime}\perp XC$ (since $B^{\prime}$ is the foot of the altitude from $B$ to $XC$), and thus $\measuredangle BB^{\prime }D=90^{\circ}$, so that $B^{\prime}\in\operatorname*{Thal}\left( BD\right) $. Also, $BB^{\prime}\perp XC$ yields $\measuredangle BB^{\prime}C=90^{\circ} $, so that $B^{\prime}\in\operatorname*{Thal}\left( BC\right) $. From $B^{\prime}\in\operatorname*{Thal}\left( BC\right) $ and $B^{\prime} \in\operatorname*{Thal}\left( BD\right) $, we see that the circles $\operatorname*{Thal}\left( BC\right) $ and $\operatorname*{Thal}\left( BD\right) $ have the point $B^{\prime}$ in common. Since they also have the point $B$ in common, this shows that the circles $\operatorname*{Thal}\left( BC\right) $ and $\operatorname*{Thal}\left( BD\right) $ intersect at the two points $B$ and $B^{\prime}$ (here we WLOG assume that $B$ and $B^{\prime}$ are distinct, which is another consequence of general position). Thus, the radical axis of these circles is $\operatorname*{Rad}\left( \operatorname*{Thal}\left( BC\right) ,\operatorname*{Thal}\left( BD\right) \right) =BB^{\prime}=BH_{XBC}$.
The same argument (but applied to $D$, $C$, $B$ and $A$ instead of $A$, $B$, $C$ and $D$) shows that $\operatorname*{Rad}\left( \operatorname*{Thal} \left( CB\right) ,\operatorname*{Thal}\left( CA\right) \right) =CH_{XCB} $. Since $\operatorname*{Thal}\left( CB\right) =\operatorname*{Thal}\left( BC\right) $, $\operatorname*{Thal}\left( CA\right) =\operatorname*{Thal} \left( AC\right) $ and $H_{XCB}=H_{XBC}$, this rewrites as $\operatorname*{Rad}\left( \operatorname*{Thal}\left( BC\right) ,\operatorname*{Thal}\left( AC\right) \right) =CH_{XBC}$.
Now, the point $H_{XBC}$ lies on both lines $BH_{XBC}=\operatorname*{Rad} \left( \operatorname*{Thal}\left( BC\right) ,\operatorname*{Thal}\left( BD\right) \right) $ and $CH_{XBC}=\operatorname*{Rad}\left( \operatorname*{Thal}\left( BC\right) ,\operatorname*{Thal}\left( AC\right) \right) $, and these two lines are distinct (since $BH_{XBC}\neq CH_{XBC}$ in general position). Thus, $H_{XBC}$ lies on two of the three pairwise mutual radical axes of the three circles $\operatorname*{Thal}\left( BC\right) $, $\operatorname*{Thal}\left( BD\right) $ and $\operatorname*{Thal}\left( AC\right) $. Consequently, $H_{XBC}$ must be the radical center of these three circles, and so must lie on the third radical axis as well. In other words,
(1) $H_{XBC}\in\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $.
The same argument (applied to $B$, $C$, $D$, $A$, $Y$ and $X$ instead of $A$, $B$, $C$, $D$, $X$ and $Y$) shows that
(2) $H_{YCD}\in\operatorname*{Rad}\left( \operatorname*{Thal}\left( BD\right) ,\underbrace{\operatorname*{Thal}\left( CA\right) } _{=\operatorname*{Thal}\left( AC\right) }\right) =\operatorname*{Rad} \left( \operatorname*{Thal}\left( BD\right) ,\operatorname*{Thal}\left( AC\right) \right) =\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $.
Also, (1) (applied to $C$, $D$, $A$ and $B$ instead of $A$, $B$, $C$ and $D$) shows that
(3) $H_{XDA}\in\operatorname*{Rad}\left( \underbrace{\operatorname*{Thal} \left( CA\right) }_{=\operatorname*{Thal}\left( AC\right) } ,\underbrace{\operatorname*{Thal}\left( DB\right) }_{=\operatorname*{Thal} \left( BD\right) }\right) =\operatorname*{Rad}\left( \operatorname*{Thal} \left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $.
Finally, (1) (applied to $D$, $A$, $B$, $C$, $Y$ and $X$ instead of $A$, $B$, $C$, $D$, $X$ and $Y$) shows that
(4) $H_{YAB}\in\operatorname*{Rad}\left( \underbrace{\operatorname*{Thal} \left( DB\right) }_{=\operatorname*{Thal}\left( BD\right) } ,\operatorname*{Thal}\left( AC\right) \right) =\operatorname*{Rad}\left( \operatorname*{Thal}\left( BD\right) ,\operatorname*{Thal}\left( AC\right) \right) =\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $.
Combining the relations (1), (2), (3) and (4), we conclude that the orthocenters $H_{XBC}$, $H_{XDA}$, $H_{YAB}$ and $H_{YCD}$ all lie on the line $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $. Thus,
(5) $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $ is the line through the four points $H_{XBC}$, $H_{XDA}$, $H_{YAB}$ and $H_{YCD}$.
(Here, we use our WLOG assumption that these four points are distinct!) Applying (5) to $X$, $C$, $Y$, $A$, $D$ and $B$ instead of $A$, $B$, $C$, $D$, $X$ and $Y$, we obtain:
$\operatorname*{Rad}\left( \operatorname*{Thal}\left( XY\right) ,\operatorname*{Thal}\left( CA\right) \right) $ is the line through the four points $H_{DCY}$, $H_{DAX}$, $H_{BXC}$ and $H_{BYA}$.
Since $\operatorname*{Thal}\left( CA\right) =\operatorname*{Thal}\left( AC\right) $, $H_{DCY}=H_{YCD}$, $H_{DAX}=H_{XDA}$, $H_{BXC}=H_{XBC}$ and $H_{BYA}=H_{YAB}$, this rewrites as follows:
$\operatorname*{Rad}\left( \operatorname*{Thal}\left( XY\right) ,\operatorname*{Thal}\left( AC\right) \right) $ is the line through the four points $H_{YCD}$, $H_{XDA}$, $H_{XBC}$ and $H_{YAB}$.
In other words,
$\operatorname*{Rad}\left( \operatorname*{Thal}\left( XY\right) ,\operatorname*{Thal}\left( AC\right) \right) $ is the line through the four points $H_{XBC}$, $H_{XDA}$, $H_{YAB}$ and $H_{YCD}$.
Compared with (5), this yields that $\operatorname*{Rad}\left( \operatorname*{Thal}\left( XY\right) ,\operatorname*{Thal}\left( AC\right) \right) =\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $.
Now, recall that if three circles $k$, $k^{\prime}$ and $k^{\prime\prime}$ satisfy $\operatorname*{Rad}\left( k,k^{\prime}\right) =\operatorname*{Rad} \left( k^{\prime},k^{\prime\prime}\right) $, then these three circles are coaxal. Applying this to $k=\operatorname*{Thal}\left( XY\right) $, $k^{\prime}=\operatorname*{Thal}\left( AC\right) $ and $k^{\prime\prime }=\operatorname*{Thal}\left( BD\right) $, we conclude that the circles $\operatorname*{Thal}\left( XY\right) $, $\operatorname*{Thal}\left( AC\right) $ and $\operatorname*{Thal}\left( BD\right) $ are coaxal. In other words, the circles $\operatorname*{Thal}\left( AC\right) $, $\operatorname*{Thal}\left( BD\right) $ and $\operatorname*{Thal}\left( XY\right) $ are coaxal. In other words, the circles with diameters $AC$, $BD$ and $XY$ are coaxal. This proves Theorem 2 (b).
If three circles are coaxal, then their centers lie on one line. Thus, the centers of the circles with diameters $AC$, $BD$ and $XY$ lie on one line (since we know that these circles are coaxal). In other words, the midpoints of the segments $AC$, $BD$ and $XY$ lie on one line (because for any $P$ and $Q$, the center of the circle with diameter $PQ$ is the midpoint of the segment $PQ$). This proves Theorem 2 (a).
Now let us prove Theorem 2 (c). We need to prove that the orthocenters of the triangles $XBC$, $XDA$, $YAB$ and $YCD$ (that is, the four points $H_{XBC}$, $H_{XDA}$, $H_{YAB}$ and $H_{YCD}$) all lie on the radical axis of any two of the circles with diameters $AC$, $BD$ and $XY$. Since we already know that these orthocenters all lie on the line $\operatorname*{Rad} \left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $, it suffices to show that the line $\operatorname*{Rad} \left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $ is the radical axis of any two of the circles with diameters $AC$, $BD$ and $XY$. In other words, it suffices to show that the line $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $ is the radical axis of any two of the circles $\operatorname*{Thal}\left( AC\right) $, $\operatorname*{Thal}\left( BD\right) $ and $\operatorname*{Thal}\left( XY\right) $. But this follows from the fact that if $k$, $k^{\prime}$ and $k^{\prime\prime}$ are three coaxal circles, then $\operatorname*{Rad}\left( k,k^{\prime}\right) $ is the radical axis of any two of the circles $k$, $k^{\prime}$ and $k^{\prime\prime}$. (We apply this fact to $k=\operatorname*{Thal}\left( AC\right) $, $k^{\prime}=\operatorname*{Thal} \left( BD\right) $ and $k^{\prime\prime}=\operatorname*{Thal}\left( XY\right) $ here). Theorem 2 (c) is thus proven.
(d) Finally, let us prove Theorem 2 (d). We already know that the line $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $ is the radical axis of any two of the circles with diameters $AC$, $BD$ and $XY$. Hence, in order to prove Theorem 2 (d), it is enough to show that, if the points $A$, $B$, $C$ and $D$ lie on one circle, then the point $AC\cap BD$ lies on the line $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $. So let us assume that the points $A$, $B$, $C$ and $D$ lie on one circle. Let $\kappa$ denote this circle. Let $Z=AC\cap BD$. Then, the two chords $AC$ and $BD$ of $\kappa$ intersect at $Z$. Thus, $ZA\cdot ZC=ZB\cdot ZD$ (according to the intersecting chords theorem), where the segments are directed.
But if $P$ is a point and $k$ is a circle, and if a line through $P$ intersects $k$ at two points $U$ and $V$, then the power of $P$ with respect to the circle $k$ is $PU\cdot PV$ (with directed segments). Applying this to $P=Z$, $k=\operatorname*{Thal}\left( AC\right) $, $U=A$ and $V=C$, we see that the power of $Z$ with respect to the circle $\operatorname*{Thal}\left( AC\right) $ is $ZA\cdot ZC$. Similarly, the power of $Z$ with respect to the circle $\operatorname*{Thal}\left( BD\right) $ is $ZB\cdot ZD$. These two powers are thus equal (since $ZA\cdot ZC=ZB\cdot ZD$), and therefore $Z$ lies on the radical axis $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $. In other words, the point $AC\cap BD$ lies on the radical axis $\operatorname*{Rad}\left( \operatorname*{Thal}\left( AC\right) ,\operatorname*{Thal}\left( BD\right) \right) $ (since $Z=AC\cap BD$). This completes the proof of Theorem 2 (d).
Nothing in the above proofs depends on the configuration of the points, as long as it is generic enough; but I wouldn't mind if someone would make a picture nevertheless :)
EDIT: See also https://problemsolversparadise.wordpress.com/2012/07/12/on-the-complete-quadrilateral-configurations/ .
It is not so difficult to prove such concurrency with trilinear coordinates.
Let $A=[1,0,0],B=[0,1,0],C=[0,0,1],H=\left[\frac{1}{\cos A},\frac{1}{\cos B}.\frac{1}{\cos C}\right]$.
In order to have $BCB'C'$ cyclic, we must have $\frac{AC'}{AB'}=\frac{AC}{AB}$, so: $$ B'=[b-\lambda c,0,\lambda a],\qquad C'=[c-\lambda b,\lambda a,0],$$ and the coordinates of the lines $BB',CC'$ in the dual space are: $$ BB'^*=[\lambda a,0,\lambda c-b],\quad CC'^*=[\lambda a,\lambda b-c,0],$$ and: $$ X = BB'\cap CC' = \left[1,\frac{\lambda a}{c-\lambda b},\frac{\lambda a}{b-\lambda c}\right].$$ So, we have just to compute the trilinear coordinates of $H'$ and check that $X\in HH'.$
We have $d\left(H',AB\right)=\frac{1}{\lambda}d(H,AC), d\left(H',AC\right)=\frac{1}{\lambda}d(H,AB)$, so: $$ H'=\left[\cdot,\frac{1}{\lambda\cos C},\frac{1}{\lambda\cos B}\right]=\left[\star,\cos B,\cos C\right],$$ giving that the circumcenter of $ABC$ belongs to the $AH'$ line. At last, we have just to compute $d(H',BC)$ in order to find $\star$ and check that $X\in HH'$. This is left to the reader since it is not so interesting, I think that the interesting part of this answer is the shown technique.
