0

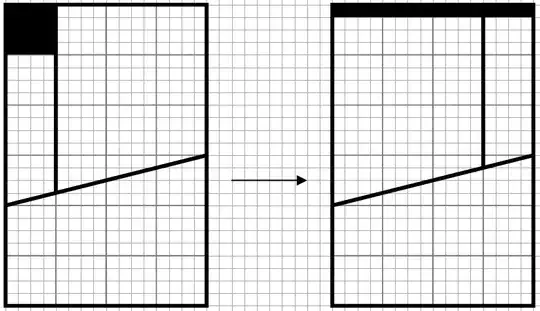
Here is a GIF image illustrating a supposedly "infinite" supply of white chocolate.

enter image description here

After watching this repeatedly, I can't definitively say why it doesn't add up. It clearly can't be infinite and the sizes of the pieces don't seem to be changed/edited. My guess is that the volume of the spaces between pieces somehow adds up to the final piece's volume.

However, the real question I have is: how have the dimensions of the array of chocolate changed? That is, if you start with a $6\times 4$ grid of chocolate pips, what are the final dimensions of the almost complete grid? I figure that height need not be considered because the cuts are made normal to the table surface.

Xoque55
  • 4,384

2 Answers2

3

enter image description here

The ending result is actually 1/5 of a piece shorter than the original bar. That amount(1/5) times 5 pieces across is equal to the extra piece

jeff
  • 285
  • This is not the same one as the OP's – user1537366 Jan 09 '15 at 02:38
  • This variation is very interesting. It is nice to see that the extra piece's area is easily verified. But what about the $6\times4$ case above? That one interests me more because the "perforated" lines seem to match up better all around. – Xoque55 Jan 09 '15 at 02:42
2

Well here's a picture:

enter image description here

Basically, the pieces that were moved end up being 1/4 shorter than they should be.

user1537366
  • 2,113