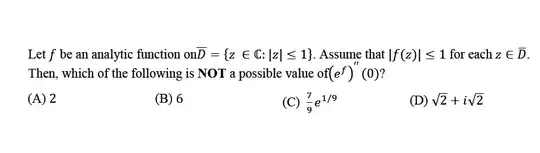
I just have answer of this question which is 6, but I don't know how to arrive at this answer. Please anyone help me solve this. How does one calculate the value of this function?
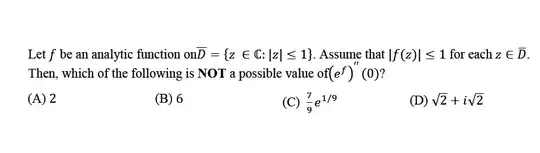
I just have answer of this question which is 6, but I don't know how to arrive at this answer. Please anyone help me solve this. How does one calculate the value of this function?
Let $g(z) = \exp(f(z))$. By Cauchy's integral formula, $$ g''(0) = \frac{2!}{2\pi i} \int_{|z|=1} \frac{g(z)}{z^{3}}\,dz $$ so by the "ML"-inequality and the estimate $|g(z)| \le e$, we have $$ |g''(0)| \le \frac{2!}{2\pi} \cdot 2\pi \max_{|z|=1} \frac{g(z)}{z^{3}} \le 2e. $$
In particular, $|g''(0)| < 6$. (All the other options are smaller in modulus than $2e$.)