Can one always map a given triangle into a triangle with chosen angles by means of a parallel projection?

Question

This is something that seems to be true from experience by playing with shadows from the sun:

If one cuts a paper triangle, he can turn it in a way to make its shadow be a triangle of any given angles (of course, not exceeding internal sum of 180°), for example: If one draws a right triangle with internal angles 90°, 60° and 30°, one can turn it in a way that the shadow triangle can be of angles 60°, 60°, 60° (equilateral) or 120°, 30° and 30° (isosceles), or any other triangle possibilities.

Is it true? How can we prove it? (if possible, showing not only that it's possible, but how to obtain the specific mapping that does it)

Answer 1

Model of the projection

Let the light come from above, along the $z$-axis. The shadow of an triangle above the $x-y$-plane is then the projection onto the $x-y$-plane ($z = 0$).

The triangle has a unit normal vector $n$ to describe its orientation ($n^2 = 1$).

The shadow projection $P$ is $$ P = \left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{matrix} \right) \quad P^c = \left( \begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{matrix} \right) $$ it satisfies $P^2 = P$ and $I = P + P^c$.

Triangle description

We specify the triangle corners by vectors $r_1$, $r_2$, $r_3$ with the origin at $0$. We define the oriented triangle sides $a_i$ as $$ a_1 = r_2 - r_1, \quad a_2 = r_3 - r_1, \quad a_3 = r_3 - r_2 $$ The side vectors are linear dependent: $$ a_1 - a_2 + a_3 = 0 $$

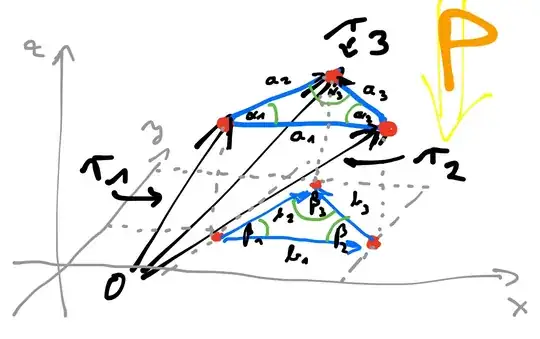
We have the angles $\alpha_i$ at the corner pointed to by $r_i$: \begin{align} a_1 \cdot a_2 &= \lVert a_1 \rVert \lVert a_2 \rVert \cos \alpha_1 \\ (-a_1) \cdot a_3 &= \lVert -a_1 \rVert \lVert a_3 \rVert \cos \alpha_2 \quad (*) \\ (-a_2) \cdot (-a_3) &= \lVert -a_2 \rVert \lVert -a_3 \rVert \cos \alpha_3 \end{align}

The equations $(*)$ are still quite general, they just relate the lengths of the sides and the angles, and embody the given orientations of the sides.

Now we get more specific: We use a triangle with these sides and $$ \lVert a_1 \rVert = 1/2 \quad \lVert a_2 \rVert = \sqrt{3}/2 \quad \lVert a_3 \rVert = 1 \quad (**) $$ and these angles $$ \alpha_1 = 90^\circ \quad \alpha_2 = 60^\circ \quad \alpha_3 = 30^\circ \\ \cos\alpha_1 = 0 \quad \cos\alpha_2 = 1/2 \quad \cos\alpha_3 = \sqrt{3}/2 $$ This assumes that the scaling of that triangle plays no role, e.g. having all sides twice the length has no qualitative influence on the problem.

To describe the $a_i$ (9 unknowns) in terms of $n$ we have these three equations $$ a_i \cdot n = 0 \\ $$ plus the three lengths $(**)$ plus the three equations $(*)$ which for this triangle are \begin{align} a_1 \cdot a_2 &= 0 \\ a_1 \cdot a_3 &= -1/4 \\ a_2 \cdot a_3 &= 3/4 \end{align}

The Shadow Triangle

The sides of the shadow triangle are $b_i$ and related via the projection: $$ b_i = P a_i $$ The projected angles are $\beta_i$ and they should satisfy equations similar to $(*)$: \begin{align} b_1 \cdot b_2 &= \lVert b_1 \rVert \lVert b_2 \rVert \cos \beta_1 \\ (-b_1) \cdot b_3 &= \lVert -b_1 \rVert \lVert b_3 \rVert \cos \beta_2 \quad (***) \\ (-b_2) \cdot (-b_3) &= \lVert -b_2 \rVert \lVert -b_3 \rVert \cos \beta_3 \end{align} We have $$ b_i \cdot b_j = P a_i \cdot P a_j = a_i \cdot a_j - a_{i3} a_{j3} \\ \lVert b_i \rVert^2 = \lVert P a_i \rVert^2 = \lVert a_i \rVert^2 - a_{i3}^2 $$ Plan: We input our $\beta_i$ into $(***)$ and get three equations for the three unknown $a_{i3}$. From this we try to determine a suitable $n$.

First case $\beta_i = 60^\circ$

The interesting bit is that $\alpha_2 = \beta_2$, which means this angle should stay the same under projection while the other two angles expand or shrink.

Looking at the equation for $\beta_2$: \begin{align} (b_1 \cdot b_3)^2 &= \lVert b_1 \rVert^2 \lVert b_3 \rVert^2 (\cos \beta_2)^2 \iff \\ \left(\frac{1}{4}+xz\right)^2 &= \left(\frac{1}{4}-x^2\right)\left(1-z^2\right)\frac{1}{4} \end{align} where $x = a_{13}$, $y = a_{23}$ and $z = a_{33}$.

This gives $$ z = \frac{\sqrt{12} x \sqrt{1- 4 x^2} - 4x}{12x^2 + 1} $$ plus we know $x - y + z = 0$.

If we have $(x,y,z)$, we can calculate all angles for the projection: \begin{align} \beta_1 &= \arccos\frac{-xy}{\sqrt{\frac{1}{4}-x^2}\sqrt{\frac{3}{4}-y^2}} \\ \beta_2 &= \arccos\frac{\frac{1}{4} + x z}{\sqrt{\frac{1}{4}-x^2}\sqrt{1-z^2}} \\ \beta_3 &= \arccos\frac{\frac{3}{4} - y z}{\sqrt{\frac{3}{4}-y^2}\sqrt{1-z^2}} \end{align} We get this graph

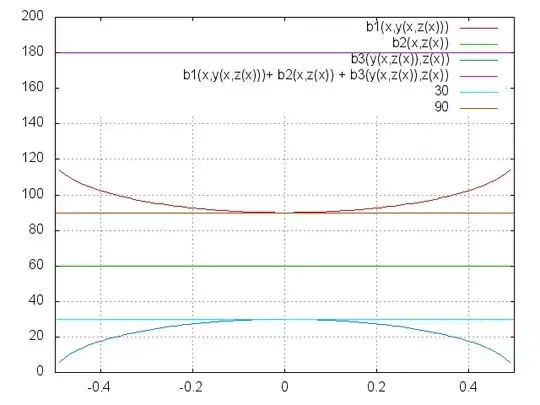
So while we can keep the projected angle at $\beta_2$ at $60^\circ$, we can not reach $60^\circ$ for $\beta_1$ and $\beta_3$. $\beta_1$ grows from $90^\circ$ and $\beta_2$ shrinks from $30^\circ$.

(At this point I could not resist to rip off a piece from the paper I did the calculations on, and folded a triangle to try it out :-)

(It looked not bad, $\beta_1$ seemed indeed growing)

I am not sure about the other cases, it is easy to make a mistake regarding the solutions, taking the wrong sign etc.

(In progress)

Answer 2

Assume that we are given a triangle $\triangle'=(A',B',C')$ in the horizontal $(x,y)$-plane, fixed up to translation, a direction $\ell$ of light, and a rigid triangle $\triangle=(A,B,C)$ that can be freely moved in $(x,y,z)$-space.

Claim: The triangle $\triangle$ can be positioned such that its shadow $\pi_\ell(\triangle)$ on the $(x,y)$-plane is homothetic to $\triangle'$.

Proof. (I) We first consider the special case that $\ell$ is vertical. When $\triangle$ and $\triangle'$ are not similar we may assume that $\gamma>\gamma'$, where $\gamma$ and $\gamma'$ denote the angles at $C$, resp. $C'$. Put $C=C'=(0,0,0)$. On the unit sphere $S^2$ draw the meridians $\mu_A$ and $\mu_B$ through $O\vee A'$ and $O\vee B'$. Let $\tilde A=(0,0,1)$ and $\tilde B\in \mu_B$ such that $\angle\tilde AO\tilde B=\gamma$. Now move $\tilde A$ continuously along $\mu_A$ towards the equator and $\tilde B$ along $\mu_B$ towards $(0,0,-1)$ in such a way that the spherical distance between $\tilde A$ and $\tilde B$ is always $=\gamma$. At any instant we can choose $A\in O\vee\tilde A$ and $B\in O\vee\tilde B$ and then have a realization of $\triangle$. Furthermore the points $A_*:=\pi_\ell(A)$ and $B_*:=\pi_\ell(B)$ lie on $\in O\vee A'$, resp. on $O\vee B'$, at all times. The distance $|OA_*|$ is zero at the beginning and has a positive end value. In a similar way, the distance $|OB_*|$ is positive at the beginning and has zero end value. It follows that we can stop the process at some moment where $${|OA_*|\over|OB_*|}={|OA'|\over|OB'|}\ .$$ (II) When $\ell$ is not vertical choose an auxiliary plane $\sigma$ orthogonal to $\ell$ and project $\triangle'$ along $\ell$ onto $\sigma$, so that a triangle $\triangle''\subset\sigma$ results. Then perform the construction described in (I), working with the movable triangle $\triangle$ and fixed triangle $\triangle''\subset\sigma$. The triangle $\triangle$ will then throw a shadow homothetic to $\triangle''$ onto $\sigma$. Removing the extra screen $\sigma$ will finally produce a shadow of the desired shape on the $(x,y)$-plane.

Answer 3

Here's an explicit solution via linear algebra.

Place both triangles on the plane with one vertex at the origin. Then we need to map the two edges going out from the chosen vertex of one triangle, call them $u_1$ and $v_1$, to the corresponding edges of the other triangle, $u_2$ and $v_2$. Both pairs of vertices are linearly independent, so there is a $2\times2$ matrix $M$ that maps $u_1$ to $u_2$ and $v_1$ to $v_2$.

This matrix has a singular value decomposition $M=U\Sigma V^T$ where $U$ and $V$ are orthogonal and $\Sigma$ is diagonal. $U$ and $V^T$ correspond to rotations and reflections in the plane, so the distortion of the triangle is encoded entirely in $\Sigma$.

Let the diagonal entries of $\Sigma$ be $\sigma_1$ and $\sigma_2$ with $\sigma_1\ge\sigma_2$. How to obtain a rigid 3D transformation whose projection to the plane is similar to $\Sigma$? Consider the matrix $\tilde\Sigma = \frac1{\sigma_1}\Sigma$ whose diagonal entries are $1$ and $\sigma_2/\sigma_1$. This is the projection of a 3D rotation about the $x$-axis by an angle of $\theta=\cos^{-1}(\sigma_2/\sigma_1)$.

So:

1. Rotate or flip the first triangle in the $xy$-plane according to $V^T$.
2. Rotate it about the $x$-axis by an angle $\theta$, taking it out of the $xy$-plane.
3. Rotate or flip it again according to $U$.

The shadow of the result is a $1/\sigma_1$-scale copy of the second triangle.

Answer 4

We'll take the special case of projection along the $z$-axis to a target triangle $\triangle A^\prime B^\prime C^\prime$ inscribed in the unit circle. Without loss of generality, we can take the triangle $\triangle ABC$ making the projection to be $$A = (1,0,0) \qquad B = (\cos2C^\prime,\sin2C^\prime, p) \qquad C = (\cos2B^\prime, -\sin2B^\prime, q)$$

for some $p$ and $q$. (The counterpart $z$ coordinate of $A$ vanishes with an appropriate vertical translation.) In accordance with the Law of Sines, we have $$\frac{|\overline{BC}|}{\sin A} = \frac{|\overline{CA}|}{\sin B} = \frac{|\overline{AB}|}{\sin C}$$ which gives a non-linear system in $p$ and $q$: $$\begin{align} p^2 \sin^2 A - ( p - q )^2 \sin^2 C + 4 \sin^2 A\sin^2C^\prime - 4 \sin^2A^\prime \sin^2 C &= 0 \\ q^2\sin^2 A - ( p - q )^2 \sin^2 B + 4 \sin^2 A \sin^2 B^\prime - 4 \sin^2 A^\prime \sin^2B &= 0 \end{align}$$

Eliminating $q$ from the system is straightforward enough, yielding a quadratic in $p^2$: $$\begin{align} 0 \quad=\quad &p^4 \sin^2 A \sin^2 B \\ - &p^2 \left(\begin{array}{c}\left(\;\sin\alpha^{+} \sin\beta^{-} - \sin\alpha^{-} \sin\beta^{+} \;\right)^2 \\ - 4 \sin^2A \sin^2B \sin^2C^\prime + 4 \sin^2A^\prime \sin^2B^\prime \sin^2 C\;) \end{array}\right) \\ - &4 \sin^2C^\prime \left(\;\sin\alpha^{+} \sin\beta^{-} - \sin\alpha^{-} \sin\beta^{+} \;\right)^2 \end{align}$$ where $$\alpha^{\pm} = A \pm A^\prime \qquad \beta^{\pm} = B \pm B^\prime \qquad \gamma^{\pm} = C\pm C^\prime$$

Because this quadratic has a non-negative leading term, and a non-positive constant term, Descartes' Rule of Signs guarantees that it has exactly one positive real root, so we can unambiguously write $$p^2 = \frac{\left(\begin{array}{c}\left(\;\sin\alpha^{+} \sin\beta^{-} - \sin\alpha^{-} \sin\beta^{+} \;\right)^2 \\ - 4 \sin^2A \sin^2B \sin^2C^\prime + 4 \sin^2A^\prime \sin^2B^\prime \sin^2 C\;) \end{array}\right) + \sqrt{\Delta}}{2\sin^2 A \sin^2 B}$$ where $$\begin{align} \Delta = \left(\; \begin{array}{c} \sin^2\alpha^{-} + \sin^2\beta^{-} + \sin^2\gamma^{-} \\ + 2 \cos\alpha^{+} \sin\beta^{-} \sin\gamma^{-} \\ + 2 \sin\alpha^{-} \cos\beta^{+} \sin\gamma^{-} \\ + 2 \sin\alpha^{-} \sin\beta^{-} \cos\gamma^{+} \end{array} \;\right) \;\cdot \left(\; \begin{array}{c} \sin^2\alpha^{+} + \sin^2\beta^{+} + \sin^2\gamma^{+} \\ + 2 \cos\alpha^{-} \sin\beta^{+} \sin\gamma^{+} \\ + 2 \sin\alpha^{+} \cos\beta^{-} \sin\gamma^{+} \\ + 2 \sin\alpha^{+} \sin\beta^{+} \cos\gamma^{-} \end{array} \;\right) \end{align}$$

The corresponding equation for $q^2$ arises by exchanging the roles $B\leftrightarrow C$, $B^\prime \leftrightarrow C^\prime$, $\beta^{\pm}\leftrightarrow\gamma^{\pm}$. (Note that $\Delta$ remains unchanged.)

Determination of the signs of $p$ and $q$ themselves is left as an exercise to the reader.