Sum of squares of Binom(n,p) values

Question

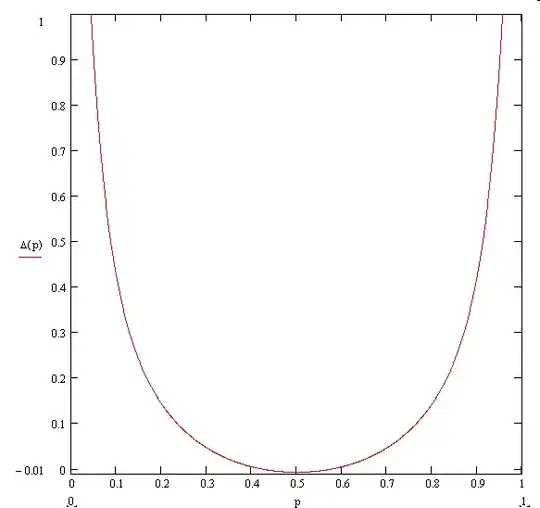
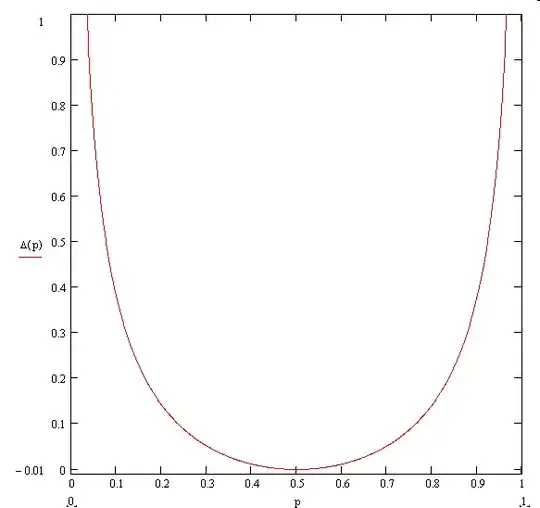
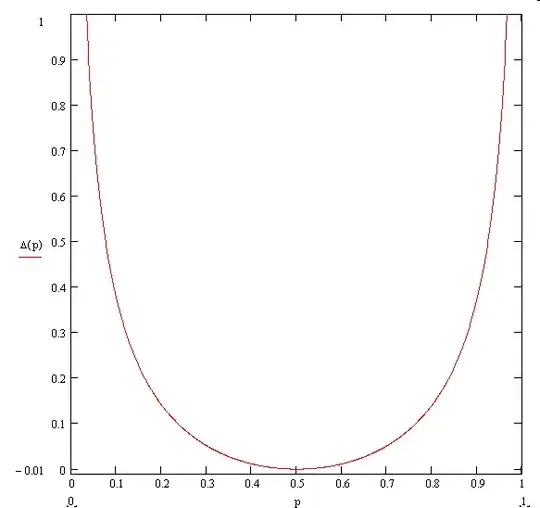
Let $x_{n,p}(j)$ be the probability that a random variable distributed according to a binomial distribution with parameters $n \in \mathbf{N}_+$ and $p \in (0,1)$ takes the value $j \in \{0,1,\ldots,n\}$, i.e. $$x_{n,p}(j)=\binom{n}{j}p^j(1-p)^{n-j}.$$ Is it true that, independently of the value of $p$, we have that $$\sum_{j=0}^n x_{n,p}^2(j)=o(1)?$$

I am aware of Vandermonde identity which implies the claim holds true for $p=1/2$: indeed $\binom{2n}{n}=\sum_{i=0}^n \binom{n}{i}^2$, so that $$\sum_{j=0}^n x_{n,p}^2(j)=\sum_{j=0}^n \binom{n}{j}^2 \frac{1}{2^{2j}}\frac{1}{2^{2n-2j}}=\frac{1}{4^n}\binom{2n}{n}=O\left(\frac{1}{\sqrt{n}}\right),$$ where the last approximation has been obtained with Stirling's formula.

Does a similar result hold in general?

Answer 1

Put $$S_n(p)=\sum_{j=0}^n x_{n,p}^2(j).$$ My calculation evidence suggests that the sequence $\{\Delta_n\}$, where $$\Delta_n(p)=\sqrt{n} S_n(p) -\frac 1{\sqrt\pi}$$ pointwise converges on $(0,1)$ to a convex function $\Delta(p)$ such that $\Delta(1/2)=0$ and $\Delta(p)= \Delta(1-p)$ for each $p$. Any suggestions about the function $\Delta(p)$?

I add graphs of functions $\Delta_n$ suggesting the convergence:

$\Delta_{10}$:

$\Delta_{100}$:

$\Delta_{1000}$: