4

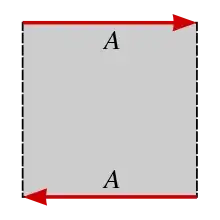
I feel like this should be simple, and it is intuitively obvious by looking at the polygon with side identifictations version of the Mobius band, but how do we explicitly show, i.e find the homeomorphism, that the boundary of the Mobius band is the unit circle $S^1$?

Thanks

Wooster
  • 3,775

3 Answers3

5

A Mobius strip can be seen as $I^2 / \sim$ where $(a,0) \sim (1-a, 1)$ for $a \in I$. See picture.

The boundary of the strip is $\{(0,i) \ \vert \ i \in I\} \cup \{(1,i) \ \vert \ i \in I\}$ as seen from the picture. But recognize that $(0,1) \sim (1,0)$ and $(0,0) \sim (1,1)$ so this forms two lines that are really halves of a loop.

So the boundary is $S^1$.

Image of Mobius Strip obtained from Mobius Strip Wikipedia Article

Chinmay Nirkhe
  • 719
  • Thank you for your answer, but what about the two vertical sides? And who could we actually turn this into an explicit homeomorphism? – Wooster Dec 29 '14 at 13:57
2

Sure. The upper half of $S^1$ starting at $(1, 0)$ is the first lap around the band, and the lower half starting at $(-1, 0)$ is the second lap.

You can actually deform the Mobius band in $\mathbb{R}^3$ such that its boundary is $S^1$. The wikipedia page has a nice section on this.

Michael Cromer
  • 2,579
1

Hint: Identify the mobius strip with $[0,1]\times [0,1]/\sim$ where the equivalence relation is $(0,x)\sim (1,1-x)$. Then try to make a map from $[0,1]$ to $[0,1]\times \{0\} \cup [0,1]\times\{1\}/\sim$ which coincide on $0$ and $1$.

Kaladin
  • 1,485