Why the differentiation of $e^x$ is $e^x?$

Question

$$\frac{d}{dx} e^x=e^x$$ Please explain simply as I haven't studied the first principle of differentiation yet, but I know the basics of differentiation.

Answer 1

Have a look at the series representation of $e^x$ which is $$e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\dots$$ Taking derivative of this gives $$\left(e^x\right)'=\left(\sum_{n=0}^{\infty}\frac{x^n}{n!}\right)'=\left(1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\dots\right)'$$ $$=1'+x'+\left(\frac{x^2}{2}\right)'+\left(\frac{x^3}{6}\right)'+\left(\frac{x^4}{24}\right)'+\left(\frac{x^5}{120}\right)'+\dots$$ $$\implies (e^x)'=\sum_{n=0}^{\infty}\left(\frac{x^n}{n!}\right)'$$Then, differentiating term by term gives us $$(e^x)'=0+1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\dots$$ $$=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\dots$$ $$=e^x$$ $$\implies \frac{d}{dx}e^x=e^x$$

Answer 2

\begin{align} \frac{d}{dx}e^x &= \frac{d}{dx}\left(1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots \right)\\ &=0+\frac{1}{1!}+\frac{2x}{2!}+\frac{3x^2}{3!}+\dots\\ &=0+1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots\\ &=0 + e^x\\ &=e^x \end{align}

Answer 3

$$e^x=\lim_{n\to\infty}\left(1+\frac{x}{n} \right)^n$$

\begin{align} \frac{d}{dx}e^x &= \frac{d}{dx}\lim_{n\to\infty}\left(1+\frac{x}{n} \right)^n\\ &=\lim_{n\to\infty}\frac{d}{dx}\left(1+\frac{x}{n} \right)^n\\ &=\lim_{n\to\infty}n\left(1+\frac{x}{n} \right)^{n-1}\cdot\frac{1}{n}\\ &=\lim_{n\to\infty}\left(1+\frac{x}{n} \right)^{n-1}\\ &=\lim_{n\to\infty}\left(1+\frac{x}{n} \right)^{-1}\cdot\lim_{n\to\infty}\left(1+\frac{x}{n} \right)^n\\ &=1\cdot e^x\\ &=e^x \end{align}

Answer 4

$$\frac{d}{dx}e^x=\lim_{h\to 0}\frac{e^{x+h}-e^x}{h}=\lim_{h\to 0}e^x\left(\frac{e^h-1}{h}\right)=e^x\lim_{h\to 0}\frac{e^h-1}{h}=e^x\lim_{h\to 0}\frac{1+h-1+o(h)}{h}$$$$=e^x\lim_{h\to 0}\left(1+\underbrace{\frac{o(h)}{h}}_{\to 0}\right)=e^x$$

Answer 5

Visual Representation of the Slope of $e^x$

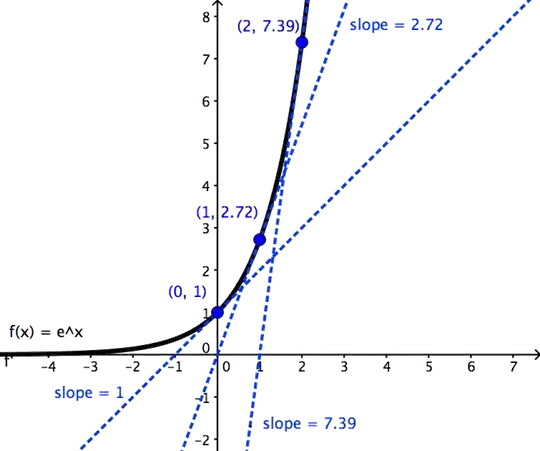
We can see that the slope is equal to $y$ at any point $(x, y)$.

Proof by Implicit Differentiation

First note that $$ \frac{d}{dx}\ln x=\frac{1}{x} $$ And $$ \frac{d}{dx}f(g(x))=\frac{d}{dg(x)}f(g(x))\frac{d}{dx}g(x) $$ So now we have $$ f(x)=e^x $$ $$ \ln f(x)=\ln e^x $$ $$ \ln f(x)=x $$ $$ \frac{d}{dx}\ln f(x)=\frac{d}{dx}x $$ $$ \frac{1}{f(x)}\left(\frac{d}{dx}f(x)\right)=1 $$ $$ \frac{d}{dx}f(x)=f(x)$$ $$ \frac{d}{dx}e^x=e^x$$

Answer 6

solving the equation $\frac{df}{dx}=f$ we get $$\frac{df}{f}=dx$$ and we obtain $$\ln|f|=x+C$$ from here we get $$f(x)=e^{x+C}$$ with $f(0)=1$ we get $$f(x)=e^x$$

Answer 7

Let $y = e^x$:

$$\begin{align*} x &= \ln y\\ \frac{dx}{dy} &= \lim_{h\to0}\frac{\ln(y+h)-\ln y}{h}\\ &=\lim_{h\to0}\ln\left(1+\frac{h}{y}\right)^\frac1h\\ &=\ln\lim_{h\to0}\left(1+\frac{h}{y}\right)^{\frac yh\cdot \frac1y}\\ &= \ln \left(e^\frac1y\right)\\ &= \frac1y\\ &= \frac1{e^x}\\ \frac{dy}{dx} &= e^x \end{align*}$$

Answer 8

The number $e$ is defined by: $e=\sum\limits_{n=0}^\infty\dfrac{1}{n!}$ but historically I think that the definition of the $exp$ function is: $e^x=\lim\limits_{n\to+\infty}\left(1+\dfrac{x}{n}\right)^n$ and the properties of this function comes from this definition as shown in this article.

Answer 9

Here is the computation of the derivative of the general $y= a^x$ where a can be any positive number. $y(x+ h)- y(x)= a^{x+ h}- a^x= (a^x)(a^h)- a^x= a^x(a^h- 1)$ So $\frac{y(x+h)- y(x)}{h}= a^x\left(\frac{a^h- 1}{h}\right)$

$\frac{da^x}{dx}= \lim_{h\to 0}a^x\left(\frac{a^h- 1}{h}\right)$ $= a^x\lim_{h\to 0}\left(\frac{a^h- 1}{h}\right)$

So the derivative of $a^x$ is $a^x$ times some constant, $\lim_{h\to 0}\frac{a^h- 1}{h}$.

It is easy to see that, if a= 1, since $a^h= 1$ for all x, that limit is 0 and if a= 3, since $3^{0.001}= 1.001099$, approximately, $\frac{1.01099- 1}{0.001}= 1.099$, there is some a, between 1 and 3, such that $\ lim_{h\to 0} \frac{a^{x+h}- a^x}{h}= 1$.

We define "e" to be that value of a so that the derivative of $e^x$ is 1 times $e^x$.