2

My question is regarding spreading $m$ vectors in an $n$ dimensional space such that the vectors are maximally distant from each other. For example, let us say I have a 2-D space, and 3 vectors, the maximally distant spread would look as follows:

enter image description here

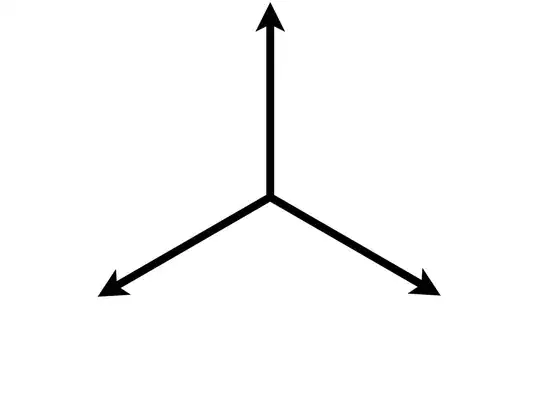
If I had 4 vectors in a 3D space it would look like this:

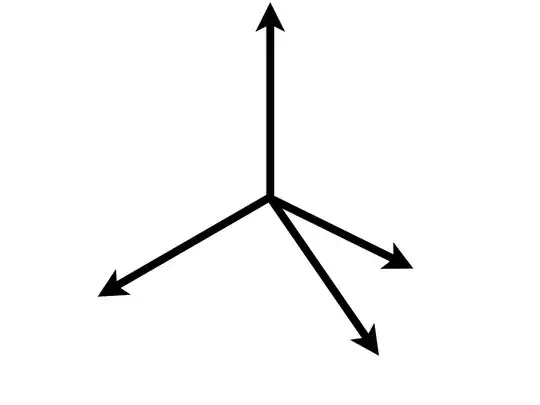
enter image description here

I'd like to know if there is a generic method to calculate a spread of vectors like this. I understand that one of the vectors would have to be given in advance so that all other $m-1$ would be aligned in relation to it.

So basically, given a vector $[v_1, v_2, ..., v_n]$ in an $n$-dimensional space I'd like to know of a way to determine what is the spread of another $m-1$ vectors such that all $m$ vectors have maximum distance between them.

Community
  • 1
WhiteTiger
  • 123
  • Are you defining the distance to be maximized as the total of the distances between all pairs of vectors, or the minimum of the distances between all pairs of vectors ? (it could possibly lead to the same result in either case) – Tom Collinge Dec 24 '14 at 07:27
  • Are we assuming that the vectors are all the same length (it appears so in the diagrams) ? – Tom Collinge Dec 24 '14 at 07:35
  • The distance to be maximized is the distance between each pair of vectors, such that the vectors should be as spread apart from each other as possible. And yes, all vectors are of the same length – WhiteTiger Dec 26 '14 at 03:43

1 Answers1

0

This is too large to be a comment.

First of all you need to define a notion of angle in your vector space. This is done in the euclidean case with the dot product, for $x,y\in\mathbb{R}^n$, this is done as: $$ \cos \theta = \frac{x\cdot y}{\|x\| \|y\|}. $$ In an arbitrary inner product vector space you could define the angle between two vectors as: $$ \cos \theta = \frac{\langle x, y\rangle}{\|x\| \|y\|}. $$ Once defined, I think what you want is to maximize the sum of the angles, i.e, given a set of $m$ unitary vectors, $\{v_i\}$, in a $n$-dimensional inner product vector space, you want to find the maximum of the function: $$ f(v_1,\dots,v_m) = \sum_{0\leq i<j\leq m} \arccos\langle v_i,v_j\rangle. $$ I think here is where your problem gets a little bit complicated, since you'll need to get some calculus involved. Write each $v_i$ in terms of a given basis (for example $v_i= a_{1i}w_1 +\cdots + a_{ni}w_n$) and maximize the above function for all such scalars.

hjhjhj57
  • 4,125
  • I had a feeling I'd need to use the dot product to get this to work, but I only have first year university calculus knowledge and what you've suggested seems to be rather complex (not that I had doubts it would be). Could you refer me to a source that could teach me the required level of calculus to solve a set of equations like that? – WhiteTiger Dec 24 '14 at 00:22
  • Also, in the case of $m$=$n$ an orthonormal basis won't do. for example, in 2D space with two vectors, to get maximum distance between them the angles would have to be 180 similarly, for 3D space with 3 vectors, the angles would be 120 – WhiteTiger Dec 24 '14 at 05:30
  • You're right. Any book on multivariate calculus will show how to find the local extrema of a multivariate function, try Stewart's for example. Even though for an arbitrary number of variables ($n\times m$ in this case) it will be quite cumbersome, conceptually it's not complicated at all. – hjhjhj57 Dec 24 '14 at 06:51