How do I evaluate the following integral $$\int_{-\infty}^{\infty} \exp\left(-\frac{\sigma^2 x^2}{2}\right) \mathrm dx\;?$$
How is it even possible to find an antiderivative?
The integral is evaluated "silently" in a book leading to a theorem.
Using Wolfram Alpha (after trying to evaluate on my own) I get
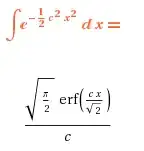
and this is not what I want, since at my level we've never worked with such a function.
Hoping someone can clarify.