Given: $f(x)=\cos(1/x)$ When $x \neq 0$ and zero at $x=0$, is: $$ F(x)= \int^x_0f(t)\,dt $$ differentiable at zero?
I believe this is differntiable, since intuitively we are shrinking the area we are integrating over so it should approach zero, but I could use a hand starting the proof.
Let $$G(x)=\left\{\begin{array}{cl}x^2\sin(1/x)&\mbox{ if }x\ne 0,\\ 0&\mbox{ if }x=0.\end{array}\right.$$ Note that $G'(x)=2x\sin(1/x)-\cos(1/x)$ for $x\ne 0$ and $G'(0)=\lim_{h\to0}G(h)/h=0$. Let $$g(x)=\left\{\begin{array}{cl}2x\sin(1/x)&\mbox{ if }x\ne 0,\\ 0&\mbox{ if }x=0.\end{array}\right.$$ Clearly, $g$ is continuous. But then $g$ is a derivative, because all continuous functions are derivatives. It follows that $$f(x)=g(x)-G'(x)$$ is the difference of two derivatives, and is therefore a derivative itself.
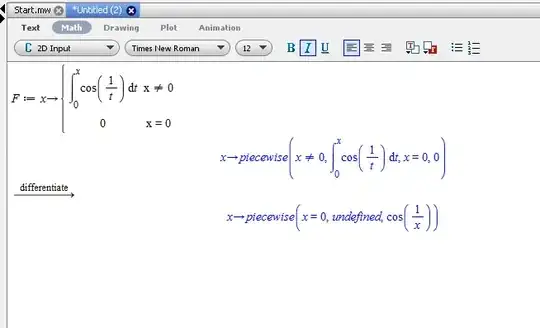
Note also that $f$ is continuous except at one point, and it is bounded, so it is Riemann integrable, and therefore $F$ is well-defined. The function $F$ is continuous at all points and an antiderivative of $f$ at all points different from $0$, but then it is an antiderivative of $f$, since the argument in the previous paragraph shows that $f$ has an antiderivative, even at $0$, and continuity prevents us from having an antiderivative of $f$ that differs from $F$ only at one point.
That $F$ is an antiderivative of $f$ can also be shown (by rescaling) as a consequence of a more general result in Chapter 14 of A second course on real variables by van Rooij and Schikhof, but the argument above is much simpler. For completeness, the result in the van Rooij-Schikhof book is the following:
Theorem. Suppose that $j:[0,\infty)\to\mathbb R$ is a derivative, and that $j(x+1)=j(x)$ for all $x\ge0$. Let $J$ be an antiderivative of $j$, and let $A=J(1)-J(0)$. Define $h$ on $[0,1]$ by $$ h(x)=\left\{\begin{array}{cl}j(x^{-1})&\mbox{ if }0<x\le1,\\ A&\mbox{ if }x=0.\end{array}\right.$$ It is then the case that $h$ is a derivative on $[0,1]$. In particular, if $k:[0,1]\to\mathbb R$ is a derivative, and $k(x)=j(x^{-1})$ for $0<x\le 1$, then $k(0)=A$.
Another approach is to simply argue that $F(x)/x\to0$ as $x\to 0$. Trying to appeal to L'Hôpital's rule does not help much here: $F(x)/x=f(c_x)$ for some $c_x$ between $0$ and $x$. One then needs to prove that $\lim_{x\to 0}f(c_x)$ exists (and equals $0$), but this is not the same as arguing that $\lim_{x\to0}f(x)=0$. Clearly, the latter would have implied the former. But the latter is false. Since we do no have much control over the function $x\mapsto c_x$ (see also here), dealing with the former directly does not seem too feasible. Instead, one is forced to argue directly in terms of the integral $F$ (as I suggested in some comments before posting this answer). This is not hard in the case at hand, and details have been worked out in the answer by poster copper.hat.
$F(x)$ is differentiable at $0$ if and only if $$ \lim_{x \to 0} \frac{F(x) - F(0)}{x-0} =\lim_{x \to 0} \frac{F(x)}{x} \stackrel{\mathcal{L}}{=} \lim_{x \to 0} F^\prime (x) = \lim_{x \to 0} f(x) $$ exists.
Now, the real question is whether or not
$$ \lim_{x \to 0} \cos(1 / x)$$
exists. I will leave that to you.
See comments below.
MAPLE says:
Here is a tedious (but elementary) approach:
We have ${F(h) \over h} = {1 \over h} \int_0^h \cos {1 \over x} dx$. Using the substitution $t={1 \over x}$ we get $\int_0^h \cos {1 \over x} dx =\int_{1 \over h}^\infty \cos t {1 \over t^2} dt$, and integrating by parts with $u = {1 \over t^2}, dv = \cos t \,dt$ gives $\int_{1 \over h}^\infty \cos t {1 \over t^2} dt = {1 \over t^2} \sin t \big |_{1 \over h}^\infty+ \int_{1 \over h}^\infty\sin t {2 \over t^3} dt$. Hence $|\int_0^h \cos {1 \over x} dx| \le |h^2 \sin {1 \over h}|+ \int_{1 \over h}^\infty {2 \over t^3} dt \le h^2+h^2$, from which we get $|{F(h) \over h}| \le 2h$, and hence $F'(0) = 0$.
