Basically, I'm asking 'Is there any place where I can access a compendium of formal mathematical proofs'? I need to know what processes mathematicians went through to declare $(-1)(-1)=1$ and so on. I believe this will actually help me understand topics a lot better.
Also, why is $y^{-1}$ = $\dfrac{1}{y^1}$?
If you want to understand these fundamentals and the book you are reading is asking you to just believe this or that 'fact', then just get rid of the book and find a good one. You are not supposed to just believe anything. There are plenty of books that will prove the fundamental results as well. Look for introductory books on analysis and/or algebra (not pre-calc or pre-algebra) and enjoy!
For now: $(-1)(-1)+(-1)=(-1)\cdot ((-1)+1)$ by distributivity. Then $(-1)\cdot ((-1)+1)=(-1)\cdot 0=0$ (but now you may want to know why $a\cdot 0=0$...
As for $y^{-1}$, that is just defined, for $y\ne 0$, to be $1/y$. The reason is that it agrees with the familiar rules for exponentiation, so there is nothing arbitrary in this definition either.
For $y \neq 0$, by using the factorization and simplifying rules we have $\frac{y}{y} = \frac{1}{y} \times y = 1$. By multiplying both side of this equation from the right hand side by $y^{-1}$ we do have $\frac{1}{y} \times y \times y^{-1} = 1 \times y^{-1} $ $\Rightarrow $ $\frac{1}{y} = y^{-1}$.
Where the last results came from the multiplication rule for exponentials; i.e. $x^{y_1} \times x^{y_2} = x^{y_1 + y_2}$.
And we are done.
I don't know if this sets the question, but basically one first observes that $a^na^m=a^{n+m}$ (this is a basic observation on the definition of multiplication). So now you have that $a^na^m=1=a^0$ implies $m=-n$. By the way, $a^0=1$ because from the previous observation one has $a^0=a^{n-n}=a^n/a^n=1$.
It might help to look at an example: $$ 2^4 = 16 $$ $$ 2^3 = 8 $$ $$ 2^2 = 4 $$ $$ 2^1 = 2 $$ Obviously, each time the exponent in the left hand side goes up by 1, the right hand side gets doubled. Or, each time the exponent goes down by 1, the right hand side gets cut in half.
Your question is, what should come next? What should you get for the values of: $$ 2^0 = ? $$ $$ 2^{-1} = ? $$ $$ 2^{-2} = ? $$ $$ \ldots $$
$$\begin{align} \vdots&\phantom{{}=1\cdot y\cdot y\cdot y\cdot y}\kern3mu\raise1mu{.}\kern3mu\raise6mu{.}\kern3mu\raise12mu{.}\\ y^4&=1\cdot y\cdot y\cdot y\cdot y\\ y^3&=1\cdot y\cdot y\cdot y\\ y^2&=1\cdot y\cdot y\\ y^1&=1\cdot y\\ y^0&=1\\ y^{-1}&=1\div y\\ y^{-2}&=1\div y\div y\\ y^{-3}&=1\div y\div y\div y\\ y^{-4}&=1\div y\div y\div y\div y\\ \vdots&\phantom{{}=1\div y\div y\div y\div y}\ddots \end{align}$$
If you use the "definition" $y^{n+1}=y\cdot y^n$ for integer powers with $y^1=y$ and roll backwards, you get $$y^1=y=y\cdot y^0$$ from which, for $y\neq 0$, $y^0=1$ then for $y\neq 0$ $$1=y^{0}=y\cdot y^{-1}$$ and the conclusion follows.
In short, this is the consistent way of extending the original definition of positive integer powers to negative integers.
$y^{-1}=\frac{1}{y}$ is a definition, but A didactic way, is use that if $a>0\implies n\log{a}=\log{a^n}$ and $\log{\frac{b}{a}}=\log{b}-\log{a}$
Then if $y>0$, then $$\log{y^{-1}}=-1\cdot\log{y}=-\log{y}$$ and $$\log\left(\frac{1}{y}\right)=\log{1}-\log{y}=-\log{y}$$
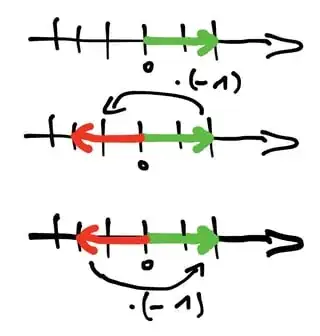
In the complex plane we have $$ -1 = e^{i\pi} $$ Multiplication by $-1$ can be interpreted as rotation by $\pi=180^\circ$. If you do this twice $(-1)(-1)$ you end up where you started $$ (-1)(-1)= e^{i\pi} e^{i\pi} = e^{i2\pi} = e^{i 0} = 1 $$ One could also argue like this without complex numbers, like this:
About the compendium: going directly to proof theory in maths and logic or formal systems in computer science seems a hard task to me.
I would rather start with some introduction math books (set theory, calculus, linear algebra, logic, formal languages and automata, ..) to get a feeling for mathematical proofs.
Here are some nice proofs: link.
Or try to get a look at a book from Bourbaki in a mathematical library, to see very good mathematicians to build up maths from scratch.
