7

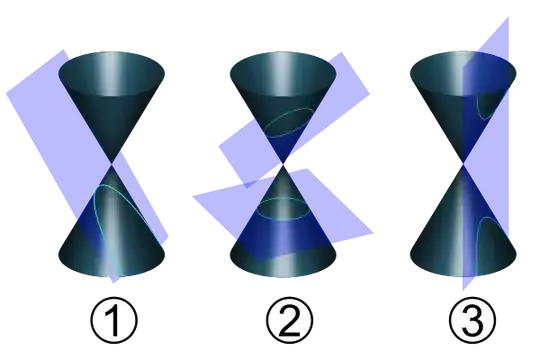
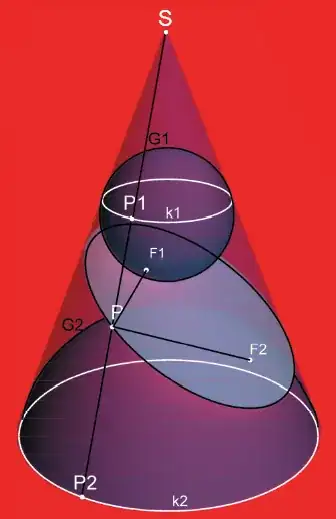
I have not been able to find a proof that the following definitions are equivalent anywhere, thought maybe someone could give me an idea:

  1. A parabola is defined geometrically as the intersection of a cone and a plane passing under the vertex of a cone that does not form a closed loop and is defined algebraically as the locus of points equidistant from a focus and a directrix.
  2. An ellipse is defined geometrically as the intersection of a cone and a plane that passes under the vertex and forms a closed loop and is defined algebraically as the locus of points the sum of whose distances from two foci is a constant.
  3. A hyperbola is defined geometrically as the intersection of a double cone and a plane that does not pass under the vertex and is defined algebraically as the locus of points that have a constant difference between the distances to two foci.

Picture of the geometric definitions: enter image description here

Elliot Gorokhovsky
  • 2,107
  • Rather than "the locus of points equidistant from two foci" you should say "the locus of points that have a constant sum of the distances to two foci". The set of points equidistance from the two foci is a line that is the perpendicular bisector of the segment connecting the two foci. ${}\qquad{}$ – Michael Hardy Dec 13 '14 at 00:24
  • @MichaelHardy ya you're right sorry – Elliot Gorokhovsky Dec 13 '14 at 00:25

1 Answers1

9

All of these can be proved by using Dandelin spheres. And Dandelin spheres can also be used to prove that the intersection between a plane and a cylinder is an ellipse.

Dandelin spheres

Both spheres in this picture touch but do not cross the cone, and both touch but do not cross the cutting plane. The points at which the spheres touch the plane are claimed to be the two foci. The distance from $P_1$ to $P$ must be equal to that from $F_1$ to $P$ because both of the lines intersecting at $P$ are tangent to the same sphere at $P_1$ and $F_1$ respectively. Similarly the distance from $P_2$ to $P$ equals that from $F_2$ to $P$. It remains only to see that the distance from $P_1$ to $P_2$ remains constant as $P$ moves along the curve.

For the hyperbola, the two spheres are in opposite nappes of the cone. For the parabola, there is only one Dandelin sphere, and the directrix is the intersection of the cutting plane with the plane in which the sphere intersects the cone.

Community
  • 1
Michael Hardy
  • 1
  • Perhaps I'm being too nitpicky, but how can we know that ellipses of every imaginable shape (eccentricity) can be created by slicing a plane in the required range of angles? From the point of view of someone trying to prove that the shapes described by both definitions are the same, this would also be required to show that all ellipses can indeed, as the cone definition says, be created by slicing a cone. The fact that the circle progressively elongates into a hyperbola suggests this intuitively, but it doesn't seem rigorous enough. Excellent answer otherwise, though! – harry Aug 16 '21 at 14:07
  • @harry : I'd start with the fact that in parameterizing the family of all shapes of ellipses, there is just one degree of freedom. – Michael Hardy Aug 16 '21 at 17:57
  • Is it the eccentricity? I'm afraid I don't know how to go on from there, either. – harry Aug 17 '21 at 13:43
  • @harry : It is the eccentricity. Maybe you should post a separate question on that, with a link to this one. – Michael Hardy Aug 17 '21 at 19:18