Is it possible for an antiderivative to exist but not to be equal to the integral?

Question

This question is about:

$$\int_0^{2\pi} \frac{1}{1.1+\cos x}$$

The solution is $20\pi/\sqrt{21}$.

But when using the antiderivative,given here I get a solution of $0$.

What is going on here?

Answer 1

The basic problem is that although there exist continuous antiderivatives, the antiderivatives given by a closed form formula have discontinuities (in this case at points where the tangent function goes to $\pm \infty$). You have to take those into account when using the Fundamental Theorem of Calculus.

EDIT: In this case the antiderivative given is $$ F(x) = \dfrac{20}{\sqrt{21}} \arctan\left( \dfrac{\tan(x/2)}{\sqrt{21}}\right)$$ The problem is that $\tan(x/2)$ has a singularity at $x = \pi$: $\tan(x/2)$ is not defined there. If you plot it, you'll see that $F(x)$ actually has a jump discontinuity:

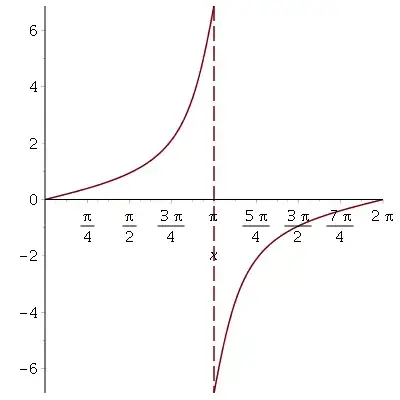
As $x$ approaches $\pi$ from the left, $\tan(x/2)/\sqrt{21}$ goes to $+\infty$, so arctan of that goes to $+\pi/2$, and $F(x)$ goes to $10 \pi/\sqrt{21}$. As $x$ approaches $\pi$ from the right, $\tan(x/2)/\sqrt{21}$ goes to $-\infty$, so arctan of that goes to $-\pi/2$, and $F(x)$ goes to $-10 \pi/\sqrt{21}$. Of course, the discontinuity means $F(x)$ is not really an antiderivative at $x = \pi$: a discontinuous function can't be differentiable. In order to get a correct antiderivative, you have remove the discontinuity, e.g. by adding $20 \pi/\sqrt{21}$ to the function on the right of $x=\pi$. Thus a correct antiderivative over this interval is $$ G(x) = \cases{\dfrac{20}{\sqrt{21}} \arctan\left( \dfrac{\tan(x/2)}{\sqrt{21}}\right) & for $x < \pi$\cr \dfrac{10 \pi}{\sqrt{21}}& for $x = \pi$\cr \dfrac{20}{\sqrt{21}} \arctan\left( \dfrac{\tan(x/2)}{\sqrt{21}}\right) + \dfrac{20 \pi}{\sqrt{21}} & for $x > \pi$\cr}$$ Here is its graph:

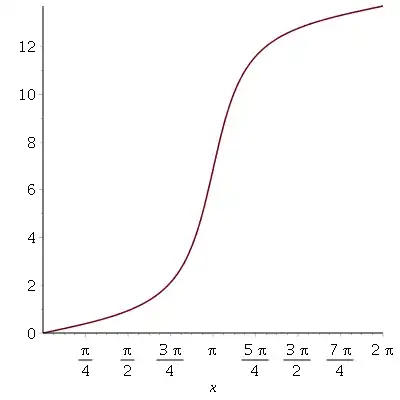
And the correct integral is $G(2\pi) - G(0) = 20 \pi/\sqrt{21}$.

EDIT: Why do we get a formula for the antiderivative that has a discontinuity where the integrand doesn't? On a deeper level, what's going on here is that the integrand has simple poles in the complex plane (at the zeros of $\cos(z) + 1.1$), and so any antiderivative will have branch cuts. When a branch cut intersect the real line we get a discontinuity.

Answer 2

See How do you integrate $\int \frac{1}{a + \cos x} dx$? and substitute 1.1 for a.

Also, Wolfram alpha gives the right answer, and it looks very similar to what you put in Symbolab. I think you may have entered the wrong number into Symbolab ($\frac{2\pi}{2}$ instead of $\frac{\pi}{2}$).

Answer 3

EDIT: following answer is incorrect. Disregard, trying to fix.

I don't know where you are getting that crazy antiderivative, but here is how I would do it.

$$\int \frac{dx}{1.1 + cos x}$$ $$x = \cos^{-1}u, \space \space dx = \frac{-1}{1-u^2}$$

$$-\int \frac{du}{(1.1 + u)(1+u)(1-u)}$$

and now we can use partial fracitonal decomposition.

$$\frac{A}{1.1+u}+\frac{B}{1+u}+\frac{C}{1-u} = \frac{1}{(1.1 + u)(1+u)(1-u)}$$

$$ A(1+u)(1-u) + B(1.1+u)(1-u) + C(1.1+u)(1+u) = 1$$

Skipping a few steps for the interest of time, $A = 4.7619, B=-5, C=0.238095$

Our integral is equal to $-4.7619 \ln |1.1 + u| +5 \ln |1+u| -0.238095 \ln|1-u|$

Plug in u = cos x.