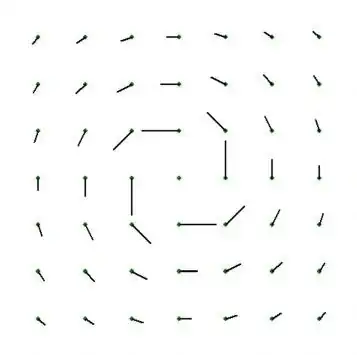
The question is:
Find the velocity of the flow described by the velocity potential given in the polar coordinates $φ$$(r, θ)$ = $θ$,
where $x = r cos θ$ and $y = r sin θ$,
$r > 0, 0 ≤ θ < 2π$
and sketch the flow.
I have no idea where to start! We have not been given a definition of the velocity potential. I feel like there is something missing from the question.
Wikipedia reference:
Flow velocities $(u,v)$ are obtained from the flow potential $\phi$ as follows: $$ u = \frac{\partial \phi}{\partial x} \quad ; \quad v = \frac{\partial \phi}{\partial y} $$ First transform to Cartesian coordinates and then take the derivatives: $$ \phi = \theta = \arctan(y/x) \quad \Longrightarrow \quad u = \frac{-y}{x^2+y^2} \; , \; v = \frac{x}{x^2+y^2} \quad \Longrightarrow \quad (u,v)= \frac{(-y,x)}{r^2} $$Wikipedia reference:
You have an irrotational vortex with strength $2\pi$ and rotating counterclockwise:
