13

I've been playing with the functions $$f_n:[0,\pi/2]\to[0,1]\\\begin{cases} f_1&=&\sin\\f_{n+1}&=&\sin\circ f_n\end{cases}.$$ A simple argument proves that $f_n(x)\to 0$ for $x\in [0,\pi/2].$ I thought it was interesting, though, how the functions did that. Near $0,$ we have $\sin\approx \operatorname{id},$ so near $0,$ iterating the sine should be close to iterating the identity function. I wanted to see what happens near zero that the function $f_n$ stops behaving like the identity function and starts behaving so as to allow the convergence of the sequence to zero. I've plotted some iterations and it looks like the functions get "broken" near zero. The point of the "breaking" seems to go to zero as $n$ goes to infinity. And the "break" seems to get more and more "severe".

I'll post some graphs of the following "normalized" functions:

$$g_n:[0,\pi/2]\to[0,1]\\g_n=\frac{f_n}{f_n(\pi/2)}$$

These functions approximate the indicator function of the domain. (I've actually seen a proof of this. My teacher showed me when I asked him, but I've already forgotten it. I remember it involved the Stolz–Cesàro theorem.) As you can see, there are points when the functions slow down abruptly. I believe the point where it happens should be the unique zero of the third derivative of $g_n.$ It is easy to see that the first derivatives of the functions are all positive and the second derivatives are all negative. However, writing down a general formula for the third derivative is difficult. I've tried doing it despite the length, but I realized that even if I finish doing it, I'll never see anything in such a long formula.

So my question is: can you see a way of proving that the third derivative of $g_n$ has a unique zero in $(0,\pi/2)$ for $n>1?$ And if so, that those zeroes converge to zero as $n\to \infty?$

EDIT: I still don't know how to prove it, but my interpretation of the pictures has changed on further reflection. It seems to me that I was wrong, and the points I'm asking about are not the zeroes of the third derivatives, but their minima (zeroes of the fourth derivatives). They are points were the speed of deceleration is the greatest, not the points where the speed of deceleration is zero. This means that there is more to prove apparently. I'm still unable to handle the third derivatives of these functions, so I can't prove that the third derivatives are negative, which I now think is true. But I can't even dream of trying to write down the formula of the fourth derivative and equate it to zero to find out something about the points.

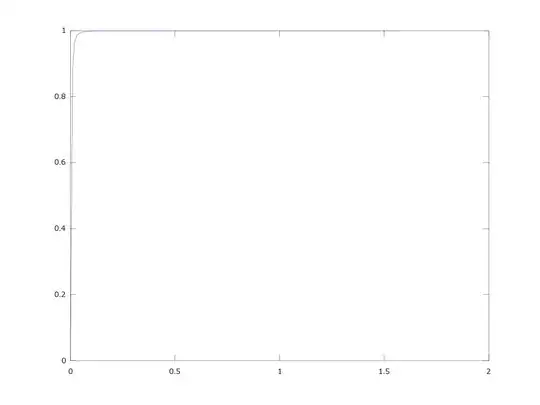
$g_1$

sin^1

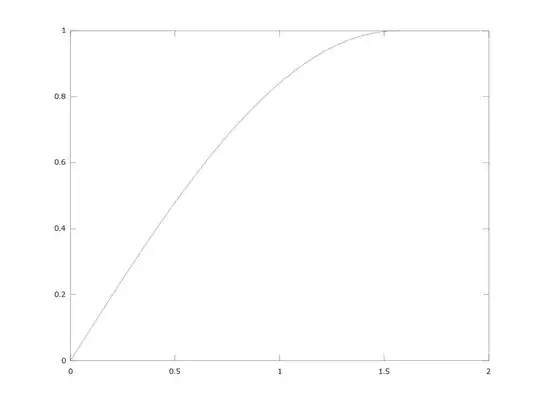
$g_{10}$

sin^10

$g_{200}$

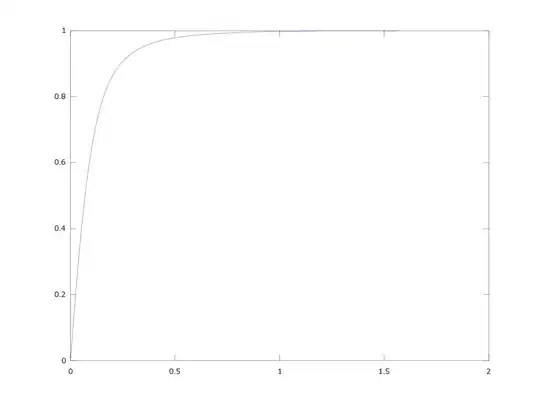
sin^200

$g_{1000}$

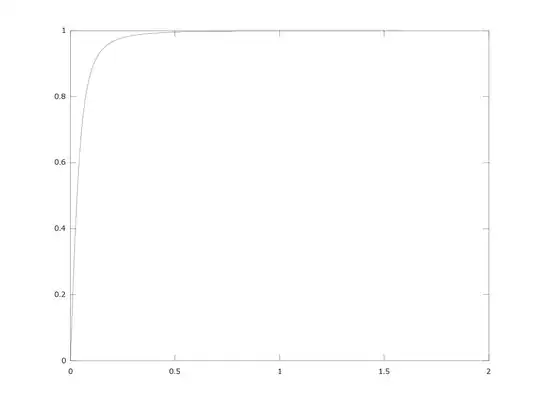
sin^1000

$g_{10000}$

sin^10000

$g_{100000}$

sin^100000

  • 1
    You might want to read this: http://math.stackexchange.com/questions/3215/convergence-of-sqrtnx-n-where-x-n1-sinx-n, perhaps it will be of interest. – Aryabhata Feb 03 '12 at 23:31
  • 2
    IIRC, de Bruijn's book"Asymptotic methods in analysis" has a chapter on the iterated sine. – marty cohen Feb 04 '12 at 06:50
  • @martycohen I'm unable access this book unfortunately. –  Feb 14 '12 at 18:56
  • The passage from de Bruijn's book can be seen in the link given in Jonas Meyer's answer to problem 14004. – daniel Feb 18 '12 at 09:48

2 Answers2

4

It is possible to explain the location of the knee in the graphs above without taking derivatives of $f_n$ or $g_n$.

Suppose that, for $x\in(0,\pi/2]$, we set $x_0:=x$, $x_{n+1}:=\sin x_n$. For all $n\ge 0$, we then have $x_n\in(0,\pi/2]$, so we can set $x_n:=\sqrt{3/t_n}$ for some $t_n=3/x_n^2$ in $[1.2,\infty)$. Expanding the Taylor series for $\sin x$ around $0$, we then have $$x_{n+1}=x_n-\frac{x_n^3}{6}+\theta_n \frac{x_n^5}{120}, \qquad 0\le \theta_n\le 1, $$ so $$t_{n+1}=t_n (1-\frac{1}{2 t_n} +\theta_n \frac{3}{40 t_n^2})^{-2}=t_n+1+O(t_n^{-1})$$ and with some computation we can find the bounds $$0\le t_{n+1}-(t_n+1)\le \frac{2}{t_n},$$ so, in particular, $t_n\ge n+1$ for all $n$ (since $t_0\ge 1.2)$, and $$0\le t_n-(t_0+n)\le \frac{2}{t_0}+\cdots+\frac{2}{t_{n-1}}\le 2 H_n,\qquad (*)$$ where $H_n$ is the $n$th harmonic number, $$H_n=1+\frac12+\cdots+\frac1n=O(\log n).$$

Now, from (*), we can see that if we iterate $\sin x$ $n$ times, starting from $x_0=\pi/2$, we will reach the value $t_n=n+O(\log n)$, or $M_n:=x_n=(1+o(1))\sqrt{3/n}$. If, as is done in the graphs above, we normalize $x_n$ by dividing by $M_n$, setting $\bar x_n:=x_n/M_n$, we get $$\bar x_n=\sqrt{\frac{n+O(\log n)}{t_n}}=(1+\frac{t_0}{n})^{-1/2} (1+O(\frac{\log n}{n})).\qquad (**)$$ Therefore, we will have $\bar x_n\approx 1$ for $t_0=o(n)$. On the other hand, if $t_0/n\to\infty$, then from (*), $t_n/t_0=1+o(1)$, so $x_n=x_0(1+o(1))$ and $\bar x_n\approx x_0/ M_n \approx x_0 \sqrt{n/3}$. The knee in the graph is located between these two regimes, which is where $t_0$ is on the order of $n$, i.e., $x_0$ is on the order of $\sqrt{3/n}$. For example, if we set $x_0=\sqrt{3/n}$ and $t_0=n$, we see from (**) that $\bar x_n\to 2^{-1/2}$ as $n\to\infty$.

David Moews
  • 16,651
3

David Moews has given a very precise analysis of the observed phenomenon. On the other hand it is very easy to prove that $$\lim_{n\to\infty} g_n(x)=1\qquad\Bigl(0<x\leq{\pi\over2}\Bigr)\ .$$ Put $\alpha_n:=f_n\bigl({\pi\over2}\bigr)$. The $\alpha_n$ converge monotonically to zero, whereby $$\lim_{n\to\infty}{\alpha_{n+1}\over\alpha_n}=\lim_{n\to\infty}{\sin\alpha_n\over\alpha_n}=1\ .$$ Given any $x\in\ ]0,1]$ there is an $r\geq 0$ with $\alpha_{r+1}<x\leq\alpha_r$. It follows that $$\alpha_{n+r+1}=f_n(\alpha_{r+1})<f_n(x)\leq f_n(\alpha_r)=\alpha_{n+r}\ .$$ Therefore we have $${\alpha_{n+r+1}\over\alpha_n}<g_n(x)\leq{\alpha_{n+r}\over\alpha_n}\ ,$$ and letting $n\to\infty$ the claim follows (note that $r$ is fixed here).

Christian Blatter
  • 226,825