21

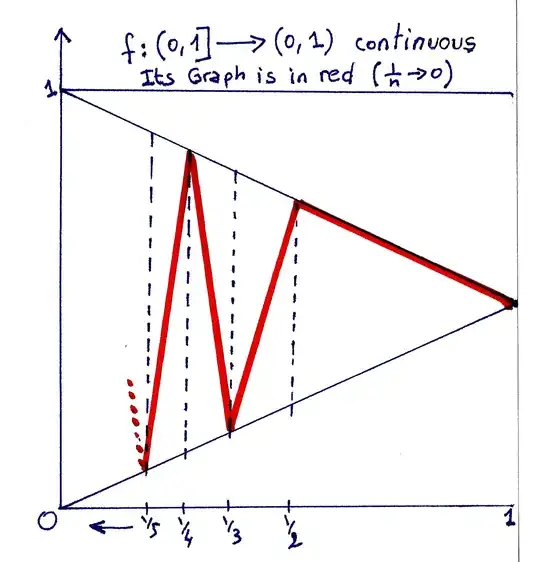
Is there any continuous function defined on $(0, 1]$ whose range is $(0, 1)$?

Winther
  • 24,478
John
  • 229
  • 2
    f cannot be uniformly continuous, or it would extend to a continuous function $F:[0,1] \rightarrow (0,1) $. – Passing By Dec 05 '14 at 03:50
  • 2
    Why would the extension have (0,1) as range and not include its limit points possibly – Aman Dec 05 '14 at 04:03
  • @Aman: If f was extended continuously into $[0,1]$ the range would have to be compact, so could not be $(0,1)$ – Passing By Dec 05 '14 at 04:06
  • 1
    @Passing By: By the same argument, I could say "There is no uniformly continuous and surjective function $f: (0,1] \to (0,1]$, because if there were, it could be extended to a continuous surjective function $F: [0,1] \to (0,1]$, which is impossible". Which is obviously false. – D. Thomine Dec 05 '14 at 12:42
  • 2
    @D.Thomine: Good point, but with a small tweak, Passing By has a very good point also. A hypothetical extension would have range $(0,1)$ or $[0,1)$ or $(0,1]$, none of which is compact. – Jonas Meyer Dec 05 '14 at 14:19
  • Ah, yes, there cannot be a continuous bijection I guess. – Passing By Dec 06 '14 at 01:24
  • @PassingBy: That is also true but not the point. An extension need not have the same image. If you add a point to the domain, it may be mapped to a point outside the original target. See Aman and D. Thomine's comments. Your first comment includes a true statement followed by an incorrect reason. – Jonas Meyer Dec 06 '14 at 20:55
  • @Jonas Meyer: But I was referring to an extension with the same range $(0,1)$ , so if we already have a continuous map from $(0,1]$into $(0,1)$ , then $f(0) \in (0,1)$, which is not compact. – Passing By Dec 06 '14 at 22:56
  • @PassingBy: You referred to such an extension, but such an imposed condition is not relevant. – Jonas Meyer Dec 06 '14 at 23:04
  • @JonasMeyer: I'm not sure I follow you, are you saying that it is possible to extend a continuous function $f :(0,1] \rightarrow (0,1)$ into a continuous $f^:[0,1] \rightarrow (0,1)$, or do you mean that my condition is not assumed or expected bythe OP? – Passing By Dec 06 '14 at 23:12
  • @PassingBy: Definitely not the first thing. I'm saying that a priori, the extra assumption that an extension would have the same range isn't justified or helpful. Sorry if I'm still unclear, but this is tangential anyway. This is my last comment here. – Jonas Meyer Dec 06 '14 at 23:17
  • Related: https://math.stackexchange.com/questions/167764 – Watson Nov 29 '18 at 20:13

4 Answers4

44

**Answer without words! see the figure **enter image description here

Idris Addou
  • 4,193
33

Something like $$x\mapsto \frac{1+(1-x)\sin(1/x)}{2} $$ will do.

hmakholm left over Monica
  • 286,031
8

Yes, there is. First send $(0,1]$ onto a spiral that winds inside a circle (e.g centered at $x=1/2$ and radius $1/2$) and then project it onto $(0,1)$.

Mirko
  • 13,445
7

$$f(x)=\frac12+\frac1\pi\arctan\left(\frac1x\cos\left(\frac1x\right)\right)$$

bof
  • 78,265