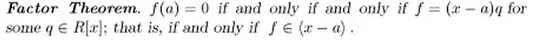 Show that the factor theorem is false in $R[x]$ if $ R $ is a noncommutative division ring.
Show that the factor theorem is false in $R[x]$ if $ R $ is a noncommutative division ring.
I started with $f = bx - ba $ where $ab \neq ba $ What should I do next?
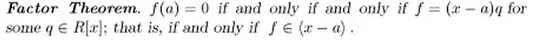 Show that the factor theorem is false in $R[x]$ if $ R $ is a noncommutative division ring.
Show that the factor theorem is false in $R[x]$ if $ R $ is a noncommutative division ring.
I started with $f = bx - ba $ where $ab \neq ba $ What should I do next?
Your example works fine:
$$f(x)=bx-ba\implies f(a)=ba-ba=0$$
If we had that $\;f(x)=(x-a)q(x)\;$ , then it must be $\;q(x)=q\in R\;$ a constant (why?) , so
$$bx-ba=(x-a)q=xq-aq\stackrel{\text{def. of identical pol's}}\implies\begin{cases}b=q\\{}\\ba=aq\end{cases}\;\implies qa=aq$$
contradicting that $\;ba\neq ab\;$ .