2

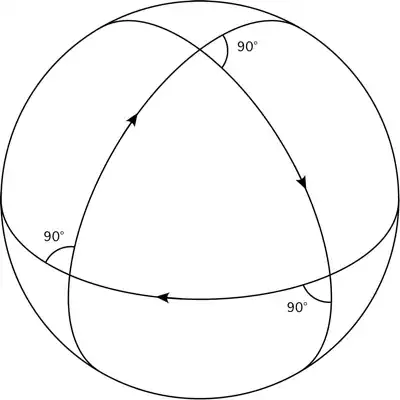
If we take a full rotation to be $360^\circ$, then it seems that we can prove the following 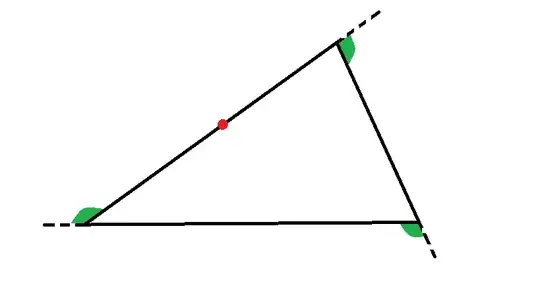enter image description here Starting from the red point, we walk clockwise along the triangle. At each vertex, we must turn through the green angles marked to proceed down the adjacent sides of the triangle. When we return to the red point, we will have turned through one full rotation. This means that the sum of the exterior angles is given as $360^\circ$, implying the interior angles of the triangle sums of $180^\circ$.

The fact that the angles of a triangle sum to $180^\circ$ is well known to be equivalent to the parallel postulate and this made me wonder whether if the fact that a full rotation being $360^\circ$ is also equivalent to the parallel postulate?

I avoided stating the question using "exterior angles of a triangle sums to $360^\circ$" and instead used the more ambiguous term "rotations" to emphasize the fact that rotations seem to be more general. We can for example show that the interior angles of a heptagram sum to $180^\circ$ by noting that three full rotations are made while "walking" thge heptagram. This should generalize to arbitrary closed polygons and seems stronger than the fact that the exterior angles sum to $180^\circ$.

In summary, I would be interested in knowing the connections that this technique has to the parallel postulate as well as if this technique is a "rigorous" way of finding the internal angles of more complex shapes such as the heptagram.

Community
  • 1
EuYu
  • 41,421
  • 1
    The parallel postulate is only false in non-Euclidean geometries. I'm not sure if it even can fail to the extent that these external angles sum to a full $360^\circ$. Angles are always defined in terms of (roughly speaking) "local rotations" so the statement is fine. – anon Jan 31 '12 at 15:27
  • http://en.wikipedia.org/wiki/Gauss%E2%80%93Bonnet_theorem#Triangles – Will Jagy Jan 31 '12 at 19:49

2 Answers2

5

Your picture, and perhaps your assumptions, are lying in the Euclidean plane. Take the same idea and put it on the sphere, where the parallel postulate is false, and we get something like the following:

90-90-90 triangle

Notice that, in this case, the sum of the exterior angles is $270^\circ$, not $360^\circ$.

However, in answer to your question about the sum of the interior angles of a polygon, since an external and the corresponding interior angle sum to $180^\circ$, the sum of the exterior angles and the interior angles is $180^\circ\times$ the number of sides. Since, as you have noted, in the Euclidean plane, the sum of the exterior angles is $360^\circ$, we get that the sum of the interior angles of a polygon with $n$ sides is $(n-2)180^\circ$.

robjohn
  • 345,667
  • To the OP: It may help you to connect this to your intuition about rotations to consider the following. Suppose you set a gyroscope rotating so that it maintains its orientation in space. You now transport the gyroscope from a certain starting point, around a closed path, and back to the same starting point. In Euclidean geometry, its orientation will be unchanged. But if you sketch it in the case supplied by robjohn, you'll see that the gyroscope's orientation is different by 90 degrees. This effect was verified empirically by Gravity Probe B: http://en.wikipedia.org/wiki/Gravity_Probe_B –  Jan 31 '12 at 16:50
  • So is the assumption I made of a full rotation consisting of 360 degrees infact equivalent to the parallel postulate? A bit of confusion for me, does that mean a circle has only 270 degrees on a sphere? – EuYu Jan 31 '12 at 17:51
  • 1
    No, locally, a complete rotation has $360^\circ$. However, the parallel postulate is not a local postulate. A triangle whose external angles sum to $270^\circ$ cannot be local. Very small spherical triangles have exterior angles that are just a bit below $360^\circ$. In fact, the sum of the exterior angles of a spherical triangle falls short of $2\pi$ radians by the area of the triangle in steradians. – robjohn Jan 31 '12 at 18:21
  • http://en.wikipedia.org/wiki/Gauss%E2%80%93Bonnet_theorem#Triangles – Will Jagy Jan 31 '12 at 19:49
  • @Will: Thanks for that link. I was having a terrible time coming up with an antonym for "excess". In that article, they use "defect", and that is about as good as any in this context. – robjohn Jan 31 '12 at 20:03
  • @robjohn you're welome. – Will Jagy Jan 31 '12 at 20:46
0

Good question. To begin with, the first part of the question is false. The "fact" that a full rotation is 360 degrees, is in fact a definition of the angular measure of a full rotation, and thus is not equivalent to the parallel postulate. You can think of it as defining what a degree is, namely, one part in 360 of a full rotation. We could have defined it to be say 100 "new degrees", but as it was, the ancients defined it as 360 degrees, presumably as a good approximation to one rotation of the earth around the sun. Thus one degree of rotation corresponds to (roughly) one day along earth's annual orbit around the sun.

For the last part of your question, indeed, this technique can be used to prove the connection between the parallel postulate and the interior angles sum of a triangle (and by extension to other polygons etc). The point is that to make your "walk clockwise along the triangle...the sum of the exterior angles is given as 360∘" statement rigorous, you need to use the parallel postulate to put all these exterior angles to the same point (ie to parallel transport all the exterior angles to one local point, and see that all the exterior angles add up to one full rotation), just that this idea is now so innate that you had implicitly assumed its validity, and as the other answers have shown, this is only true on the Euclidean plane.

CS Tong
  • 1