2

Hopefully no duplicate of Ellipse $3x^2-x+6xy-3y+5y^2=0$: what are the semi-major and semi-minor axes, displacement of centre, and angle of incline? (see below)

Let the following equation $$x^2 - \frac{1}{2}xy + y^2 - 11x - y = 18$$ be the ellipse in question. Plotting it on Webgraphing.com yields some nice values, e.g. the center at $(6, 2)$, but also the major/minor axis, which is what I am interested in. Their length is $\approx9.24$ and $\approx 7.16$ respectively.

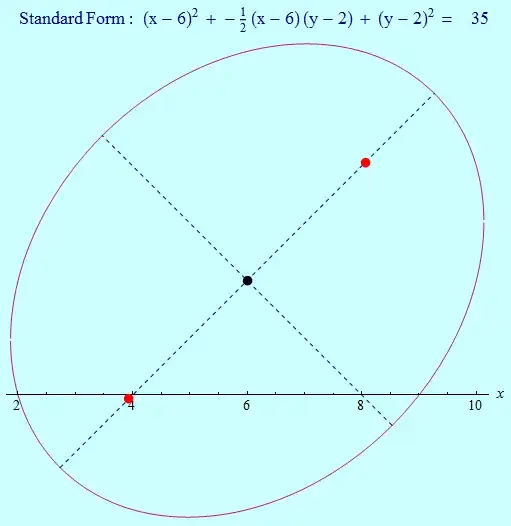
Ellipseplot

Calculating the center is no problem, but I never get the axis length right. If anyone could spot the mistake in the following calculation, that would be very helpful!

Let $A = 1 (x^2)$, $B = -\frac{1}{2} (xy)$, $C = 1(y^2)$ and $D = 18$.

The matrix $$ \left(\begin{matrix} A - \lambda & \frac{B}{2} \\ \frac{B}{2} & C - \lambda \end{matrix}\right) = \left(\begin{matrix} 1 - \lambda & -\frac{1}{4} \\ -\frac{1}{4} & 1 - \lambda \end{matrix}\right) $$ yields the eigenvalues $\lambda_{1,2} = 1 \pm \frac{1}{4}$ and the corresponding eigenvector matrix $$ \frac{1}{\sqrt{2}}\left(\begin{matrix} 1 & -1 \\ 1 & 1 \end{matrix}\right) $$

It is obvious from the above image that the vectors point in the right direction. But when attempting to calculate their lengths, I never get the right result. I somewhere read that the absolute value in the equation ($D$) had to be normalised somehow, and the eigenvalues don't have the right proportion, so I took their root. This results in the lengths $$l_1 = 2 * \sqrt{\lambda_1} * \sqrt{D} = 2 * \sqrt{\frac{5}{4}} * \sqrt{18} \approx 9.48 \neq 9.24$$ $$l_2 = 2 * \sqrt{\lambda_2} * \sqrt{D} = 2 * \sqrt{\frac{3}{4}} * \sqrt{18} \approx 7.34 \neq 7.16$$ that do not yield the correct result when printed (the red dots were the basis for the equation):

Ellipse2

For other ellipses, the error is much bigger. Can anyone point out where I am wrong in the calculation?

Concerning the thread linked above (that answers the question for another example), the method described there does not work for me (I may be applying it wrong):

$$\sqrt{\frac{35}{\lambda_2}} = \sqrt{\frac{35}{1 - \frac{1}{4}}} \approx 6.83 \neq 9.24$$

Glorfindel
  • 3,955
Brokenmind
  • 23

2 Answers2

0

You need to center the conic to get the correct RHS constant.

From $\frac349.24^2\approx\frac547.16\approx64$, I conclude that it must be $16$.

  • Your conclusion is exactly right! I didn't know that the conic needs to be centered, or that the center coordinate is directly related to that the calculation of the new RHS. Now every ellipse is displayed correctly! – Brokenmind Nov 25 '14 at 17:12
  • To extract the axis from the normalized equation, you need to center and rotate the raw equation. –  Nov 25 '14 at 18:35
0

The equation of the equation centred at the origin is $$(x+6)^2-\frac12 (x+6)(y+2)+(y+2)^2-11(x+6)-(y+2)=18\\ x^2+y^2-\frac12 xy=34$$ The quadratic coefficient matrix is $$\left(\begin{array}{cc}1 & -\tfrac14 \\ -\tfrac 14 & 1 \end{array}\right)$$ The resulting characteristic equation is $$\left|\begin{array}{cc}1-\lambda & -\tfrac14 \\ -\tfrac 14 & 1-\lambda \end{array}\right|=0\\ 16\lambda^2-32\lambda+15=0\\(4\lambda-3)(4\lambda-5)=0\\\lambda=\frac34,\frac54\qquad \text{(eigenvalues)}$$ The equation of the "untilted" ellipse is $$\tfrac34 x^2 +\tfrac54 y^2=34\\ \frac{x^2}{\left(2\sqrt{\tfrac{34}3}\right)^2} +\frac{y^2}{\left(2\sqrt{\tfrac{34}5}\right)^2}=1$$ Hence semi-major and semi-minor axes are $$2\sqrt{\frac{34}3}, 2\sqrt{\frac{34}5}$$ respectively.

It can easily be shown that the corresponding eigenvectors are $(m,m)$ and $(-m,m)$ respectively, thus the directions of the major and minor axes are $\pi/4$ and $-\pi/4$ respectively. $\blacksquare$

Hypergeometricx
  • 22,657