2

As the title says.. it says to use the mean value theorem but I don't see how that's applicable.

Thank you

Martin Sleziak
  • 53,687
user121937
  • 575
  • Compare derivatives – Alex G. Nov 23 '14 at 21:03
  • Are you allowed to use derivatives? Then it would be easy to notice that $x - \sin (x)$ is increasing. – ploosu2 Nov 23 '14 at 21:05
  • why is $x$ limited to $0$ and $\pi/4?$ is this not true for all $x \ge 0?$ – abel Nov 23 '14 at 21:25
  • @abel Maybe because then the geometric picture makes more sense. – ploosu2 Nov 23 '14 at 21:26
  • @ploosu2, geometric makes still makes sense for any $x \ge 0$ as long as you interpret $\sin (arc)$ as the $y$ coordinate of the terminal point of the arc with the initial point of the arc at $(1,0).$ – abel Nov 23 '14 at 21:29
  • @barak manos, i dont think you know what you are talking about. – abel Nov 23 '14 at 21:31
  • Related posts: http://math.stackexchange.com/questions/125298/how-to-strictly-prove-sin-xx-for-0x-frac-pi2 http://math.stackexchange.com/questions/936166/prove-sinx-x-when-x0-using-lmvt http://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 – Martin Sleziak Dec 01 '14 at 18:31

3 Answers3

6

I just propose a geometric proof:

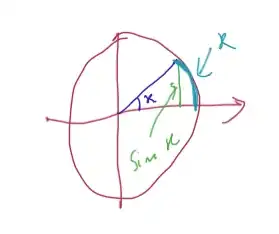
enter image description here

idm
  • 11,824
  • 2
    I'm going to upvote this (because it really is almost trivial geometrically) in spite of the terrible drawing...:) +1 – Timbuc Nov 23 '14 at 21:08
1

Hint:

$$f(x):=\sin x-x\implies f'(x)=\cos x-1\le 0$$

so $\;f\;$ is monotone descending, so

$$f(x)\le f(0)$$

Timbuc
  • 34,191
1

At $x=0$, $f(x)=x- \sin(x)$ evaluates to $0$.

Try to do a proof by contradiction.

So lets suppose there was some point $c>0$ so that $f(c) < 0$. Apply Mean Value Theorem to the interval $[0,c]$ and conclude that the there exists some $a \in [0,c]$ so that $f'(a)<0$.

But now compute $f'(x)$ as a function. You will see that it must always be positive. Hence, this contradicts that $f'(a)>0$ so there does not exist such a $c$ above. Thus we have the desired equality.

Alexander
  • 4,292
  • There's no need to phrase this as a proof by contradiction. Your approach shows directly that $f(x) \ge 0$ for any $x \in [0,\pi/4]$. – Santiago Canez Nov 23 '14 at 21:38
  • @SantiagoCanez I adopted such a phrasing because I wanted to use Mean Value Theorem. Doesn't MVT require something like a proof by contradiction here? – Alexander Nov 23 '14 at 22:16