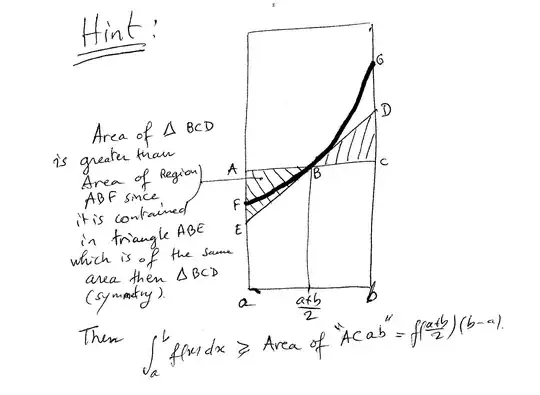
Let $f$ be continuously differentiable on $[a,b]$. If $f$ is concave up, prove that
$$(b-a)\cdot f\left(\frac{a+b}{2}\right)\le \int_{a}^{b}f(x)dx.$$
I know that (and have proved) $$(b-a)\cdot f\left(\frac{a+b}{2}\right)= \int_{a}^{b}f(x)dx$$ for any linear function on $[a,b]$. Also, the graph of $f$ lies above the tangent line at $(\frac{a+b}{2},f(\frac{a+b}{2}))$.
Let $c = (a+b)/2$.
Then use the mean value theorem and convexity.
For $x \in [a,b]$ we have $f(x) = f(c) + f'(\eta_x)(x-c)$ with $\eta_x$ between $c$ and $x$.
There are points $a < \xi_1 < c < \xi_2< b$ such that $f'(\xi_2) > f'(\xi_1)$ (by convexity) and
$$\int_a^bf(x)\,dx = \int_a^c[f(c) + f'(\eta_x)(x-c)]\,dx+\int_c^b[f(c) + f'(\eta_x)(x-c)]\,dx\\=f(c)(b-a) + f'(\xi_2)(b-a)^2/8 - f'(\xi_1)(b-a)^2/8\geq f(c)(b-a)$$
Note that the mean value theorem for integrals gives us
$$\int_c^bf'(\eta_x)(x-c)dx=f'(\xi_2)\int_c^b(x-c)dx=f'(\xi_2)(b-a)^2/8,$$
and
$$\int_a^cf'(\eta_x)(x-c)dx=f'(\xi_1)\int_a^c(x-c)dx=-f'(\xi_1)(b-a)^2/8,$$
As you noted, $f$ is convex, implies that $f$ lies above its tangent lines. The tangent line at the midpoint of the interval is $$g(x) = f'\left(\tfrac{a+b}2\right)\left(x-\tfrac{a+b}2\right)+f\left(\tfrac{a+b}2\right)$$
Now $f(x) \ge g(x)$ integrated over $[a, b]$ gives you the result.
Let $h(x)=f(x)-m x$ where $m=f'(\frac{b+a}2)$. By the Mean Value Theorem for integrals (also related to average value of a function), there is $c\in(a,b)$ such that $h(c)(b-a)=\int_{a}^{b}h(x)dx$. Note that $h$ is concave up and $h'(\frac{b+a}2)=0$ hence $h$ has a global (over $[a,b]$) minimum at $\frac{b+a}2$. Hence $h(c)\ge h(\frac{b+a}2)$. In other words $\frac1{b-a}\int_{a}^{b}h(x)dx\ge h(\frac{b+a}2)$. Thus $\frac{1}{b-a}\int_{a}^{b}h(x)dx = \frac1{b-a}(\int_{a}^{b}f(x)dx - \frac{m}{2} (b^2-a^2))= \frac1{b-a}\int_{a}^{b}f(x)dx - {m}\frac{b+a}{2}\ge$ $h(\frac{b+a}2)=f(\frac{b+a}2)-{m}\frac{b+a}{2}$ from which we obtain $\frac1{b-a}\int_{a}^{b}f(x)dx\ge f(\frac{b+a}2)$.
