Insired by this question,
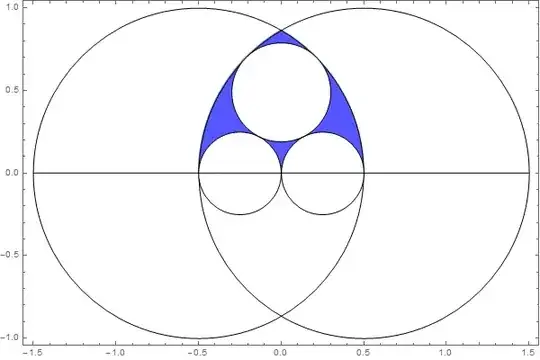
where the objective is to calculate the shaded area in the above diagram, I noticed that the inscribed circle has the following relation to the circles it rests on
\begin{align} &\sqrt{1-\left(x\pm\frac{1}{2}\right)^2}\\ &\sqrt{\frac{1}{16}-\left(x\pm\frac{1}{4}\right)^2}\\ &\pm\sqrt{c^2-x^2}+c\sqrt{\frac{1}{2 c}+1}\\ \end{align}
with the centre of the circle at
\begin{align} \left\{0,\sqrt{\frac{\frac{1}{c}+2}{\left(\frac{1}{c}+4\right)^2}} \left(\frac{1}{c}+4\right) \dfrac{c}{\sqrt{2}}\right\} \end{align}
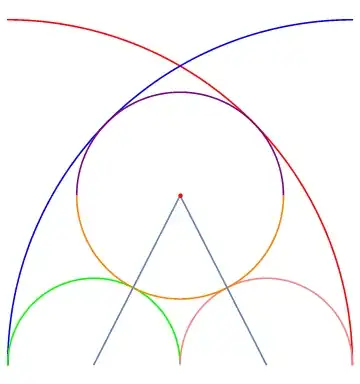
given in cartesian cordinates, where the $c=\dfrac{3}{10}$ in the first diagram shown. For varying $c$, the plot looks like this:
This relation then, can be used as the beginnings of a bit of circle packing:

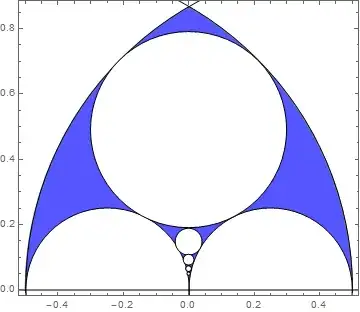
though the exact values of $c$ here are estimated, and as yet, unknown.
I can't really describe how I found this relation though, other than by chance, and looking at number patterns. Why does this work, and what are the values of $c$ as per the circles of Descartes (shown below) for the infinite packing? Can this same approach be extended to filling all of the gaps?
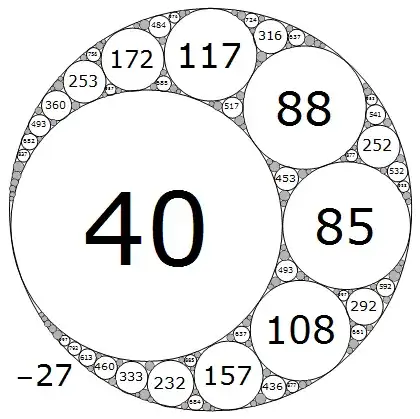
(Image from Wolfram Demonstrations, by Ed Pegg Jr)