9

Let $s,z$ be two complex variables, $\zeta(s)$ be the Riemann $\zeta$-function. Let

\begin{equation} \zeta_1(s)=\pi^{-s/2}\Gamma\left(\frac{s}{2}\right)\zeta(s), \end{equation}

be the Gamma-completed Riemann zeta function, and let

\begin{equation} f(s)=\zeta_1(s+1/2)-\zeta_1(s-1/2) \end{equation}

It satisfies the functional relation $f(s)=-f(1-s)$

Let \begin{equation} F(z)=f(iz+1/2) \end{equation}

Taylor proved in 1945 (On the Riemann Zeta function) that all the zeros of $F(z)$ are real.

We plotted $Re(F(x+I y))=0$ and $Im(F(x+I y))=0$ in Mathematica 9.0.

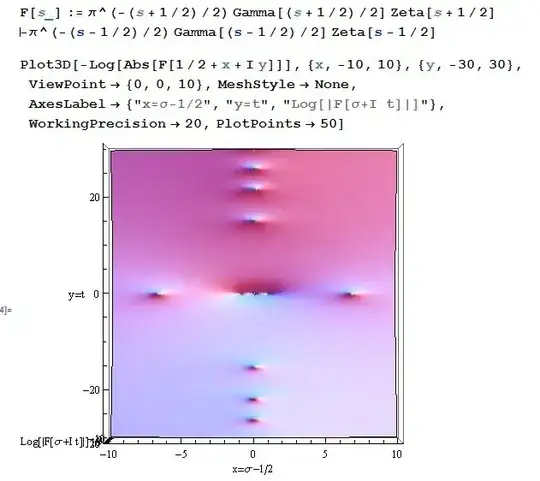
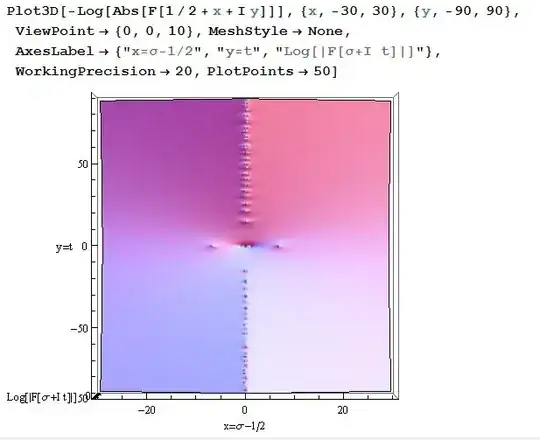
enter image description here enter image description here

We found out that at $x=0,y=\pm 6.8246$, $F(x+I y)=0$. Thus $F(z)$ seemed to have non-real zeros.

Has anyone notice this problem?

EDIT: Here is a snapshot of Taylor's formulas. enter image description here

Here is a little more enter image description here

mike
  • 5,604
  • 1
    Here's an approximation for the root: $$\begin{multline}z = 1.3179490483476020312550822896459296949554671129638*10^{-63} + \ 6.8246178956306702512881753455550038029953841561527i\end{multline}$$ and $F(\Im(z)i) \approx 10^{-49}$. (ed ajf) – Alexander Vlasev Nov 21 '14 at 09:02
  • 1
    This paper says that $\zeta_1(s) = \pi^{s/2}\Gamma(s/2)\zeta(s)$ and not as you have $\pi^{-s/2}$. – Alexander Vlasev Nov 21 '14 at 09:52
  • 1
    An MO question has it as per the OP. http://mathoverflow.net/questions/7656/why-does-the-gamma-function-complete-the-riemann-zeta-function. – daniel Nov 21 '14 at 11:31
  • @AleksVlasev. I think that the minus sign in my problem is correct. When I define another function with the positive sign, the pattern is completely different. And G(z) has non-real zeros as well. Please see the update of the figures. – mike Nov 21 '14 at 11:55
  • I think Taylor's paper is a good source for what Taylor intended. The extra plot using $\pi^{s/2}$ makes this more confusing. Since Titchmarsh had his hand in this...it would be good to read the paper carefully. – daniel Nov 21 '14 at 12:12
  • 1
    @daniel. Thanks for the suggestion. I just deleted extra plots associated with $\pi^{s/2}$ and $G(z)$. – mike Nov 21 '14 at 12:12
  • 1
    @AleksVlasev I double checked the formula in the paper you linked. It reads $\zeta_1(s) = \Gamma(s/2)\zeta(s)/\pi^{s/2}$. So this formula is identical to what I had in the OP. – mike Nov 21 '14 at 12:27
  • 1
    @mike that's quite interesting. You are right. The function with the positive sign has a zero at about

    $$z = 62.5105378688927205436579804976 i$$

     – Alexander Vlasev Nov 21 '14 at 19:51
  • Let $\sigma+i t=s=1/2+i z=1/2+ix -y$. Here $\sigma,t,x,y\in\mathbb{R}$. Thus $\sigma=1/2-y,t=x$. All zeros of $f(s)$ lie on $\sigma=1/2$ are equivalent to all zeros of $f(s)$ lie on $y=0$. Thus all zeros of $F(z)=F(x+i y)$ are real. – mike Nov 22 '14 at 04:26

2 Answers2

3

The paper simply says that all the non-real zeros of $F(s)$ lie on the line $\sigma = 1/2.$ The latest images posted by OP seem to show just that. There are non-real zeros at $\sigma = 1/2$ and two zeros located symmetrically about that line at $t = 0.$ These last have imaginary component $t = 0$ so the assertion of the theorem doesn't address them.

I went back and looked at this again, not to beat a dead horse but because I am interested in the sort of trompe l'oeil that occurred here.

The reasoning behind the question about the paper's claim was:

Let σ+it=s=1/2+iz=1/2+ix−y. Here σ, t, x, y ∈ R. Thus σ = 1/2 − y, t = x. All zeros of f(s) lie on σ = 1/2 are equivalent to all zeros of f(s) lie on y = 0. Thus all zeros of F(z) = F(x+iy) are real. –

It's an inviting idea and seems to simplify things but it mis-states the claim of the paper, which is that "all complex zeros of F(s)...lie on the line $\sigma = 1/2.$"

This took a while to see because one automatically focuses on the particulars of the transformation: is the claim of equivalence correct? Well, it is. The transformation gives a valid new picture of the same information but then we misinterpret the appearance of complex zeros.

The transformation takes the original points (x,y) of $G(s)$ and assigns new coordinates $(\hat{x},\hat{y}):$

$\hat{x} = y;$

$\hat{y}=1/2 - x;$

So when two complex zeros are found in the new system at $(0,\pm 6.82)$ these correspond to points in the original system at about $(7.32,0),(6.52,0)$ as a quick check of the graph confirms. The sequence of complex zeros on the line $x = 1/2$ in the original system are mapped to a sequence of real zeros $(x_i,0)$ in the new system.

The images posted by @mike confirm this.

daniel
  • 10,141
  • please see the 3D plot that I made using your $F(s)$. – mike Nov 22 '14 at 05:55
  • 1
    @mike: I have gone back and forth about this but your most recent plots of the function as given in the paper seem to confirm the assertion in the paper--that all the complex zeros lie on the line 1/2. The two exceptions seem to be real numbers, (a,0),(b,0). – daniel Nov 22 '14 at 09:34
  • 1
    To be nit-picky, all numbers in $\mathbb{C}$ are complex. I'm sure the language "non-real zeros" would have avoided the problem. – Alexander Vlasev Nov 22 '14 at 09:39
  • 2
    @AleksVlasev: Nit-picky but correct. I will edit to reflect this, thanks. – daniel Nov 22 '14 at 09:43
3

Here is a 3D plot of daniel's function $F(s)=F(\sigma+i t)=F(1/2+x+i y)$. The dots that pops out of the figure are the zeros because I am plotting $-\log|F(s)|$ vs. $s$.

enter image description here

It seems to me that these two zeros that are not on the $\sigma=1/2$ line are the only exceptions. See two figures below.

enter image description here enter image description here

mike
  • 5,604