11

Suppose that $f:X \to Y$ is an onto function. Prove that for all subsets $B$ subset of $Y$, $f(f^{-1}(B)) = B$. I don't know how to do this if the function is not also one to one, which it is not. Any help proving this would be greatly appreciated.

DeepSea
  • 77,651
Tud-Girly
  • 121

4 Answers4

7
  • $\exists$ is the symbol for "there exists."
  • $\wedge$ is the symbol for "and."
  • $f:X\twoheadrightarrow Y$ is notation for "$f$ is a surjective (onto) function from $X$ to $Y$."
  • $\mathcal{P}(Y)$ is notation for "powerset of $Y$" or "the set of all subsets of $Y$."

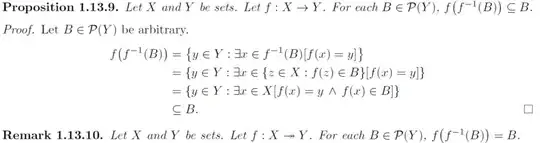
  • "$\subseteq$" becomes "$=$" for onto functions.
Alberto Takase
  • 3,511
5

Note that:

  1. For any $y\in f(f^{-1}(B)$, there exists $x \in f^{-1}(B)$ satisfying $y=f(x)$. Clearly $y=f(x) \in B$.

  2. For any $y\in B$, since $f(x)$ is an onto function, there is $x\in X$ satisfying that $f(x)=y$, i.e.,$x\in f^{-1}(y)$. So $y=f(x)\subset f(f^{-1}(y)) \subset f(f^{-1}(B)).$

rae306
  • 9,742
Paul
  • 20,553
  • I would further elaborate on second point why it is true. If f is not an onto function , then it does not necessary mean there exists x satisfying $f(x)=y$. For this case B will never be a subset of $f(f^-1(B))$ , that’s why the fact that f is onto function is important. – Nothing Jul 24 '18 at 20:02
1

Given $f : X \to Y$, and $\forall y \in Y \exists x \in X (f(x) = y)$.

Want to show that $\forall B \subset Y, f(f^{-1}(B)) = B$

We know that $f^{-1}(B) = \{ b : f(b) \in B \}$. If this set is never empty, then we have our result. The set is never empty by our second assumption.

Jonny
  • 2,519
1

First, $f^{-1}(y) = \lbrace x \in X : f(x) = y)\rbrace $. If $y \in B$, so exist $x \in X$ that $f(x) = y$ (f is onto), then $f(f^{-1}(y)) \in B$, by definition, so $f(f^{-1}(y)) \subset B$. Now, $y \in f(f^{-1}(B))$, how f is onto exist $x \in f^{-1}(B)$, such that $f(x) = y$, then $y \in B$, so $f(f^{-1}(B)) \subset B$.

Charles
  • 11