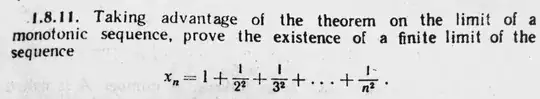
I could just prove that the sequence is bounded but couldn't find the exact limit.
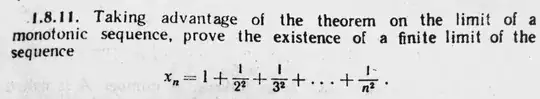
I could just prove that the sequence is bounded but couldn't find the exact limit.
The series is (obviously) $\sum\limits_{i=1}^\infty \frac{1}{n^2}$. And thus $\lim_{n \to \infty} \sum\limits_{i=1}^\infty \frac{1}{n^2} = \frac{pi^2}{6}$. See also the hyperharmonic/p-series for more information. This problem is called Basel problem. See wikipedia for a detailed proof.