I want to perform Monte Carlo simulation for the analysis of a circuit problem, where the generation of random symmetric unitary matrices "close" to
\begin{equation}T=\left[ {\begin{array}{*{20}{c}} {}&{{I_n}} \\ {{I_n}}&{} \end{array}} \right]\end{equation}
is required. $I_n$ is the identity matrix of order $n$.
There are some literature discussing how to generate random symmetric unitary matrices, such as Ozols. I figured out a way of obtaining these random matrices based on the one described by Ozols, which seems viable. However I'm not sure about its statistical interpretation, or is it "random" enough?. Can someone please make some comments or point out a direction? Thanks a lot for taking time to read this!
Here are the MATLAB codes:
[Q,R]=qr(T+sig*(randn(2*n)+1i*randn(2*n)));
RD=diag(R);
L=diag(RD./abs(RD));
Tr=Q*L;
U=Tr.'*T'*Tr;
When $n=2$ and sig=$\sqrt{0.001}$, $U$ were generated 10,000 times, with the mean value
\begin{equation}E[U]=\left[{\begin{array}{*{20}{c}} {{\rm{ - 0}}{\rm{.0003 - 0}}{\rm{.0000i}}}&{{\rm{ - 0}}{\rm{.0006 - 0}}{\rm{.0000i}}}&{{\rm{0}}{\rm{.9955 + 0}}{\rm{.0004i}}}&{{\rm{0}}{\rm{.0001 + 0}}{\rm{.0005i}}}\\ {{\rm{ - 0}}{\rm{.0006 - 0}}{\rm{.0000i}}}&{{\rm{ 0}}{\rm{.0003 - 0}}{\rm{.0001i}}}&{{\rm{ - 0}}{\rm{.0002 + 0}}{\rm{.0006i}}}&{{\rm{0}}{\rm{.9955 + 0}}{\rm{.0000i}}}\\ {{\rm{0}}{\rm{.9955 + 0}}{\rm{.0004i}}}&{{\rm{ - 0}}{\rm{.0002 + 0}}{\rm{.0006i}}}&{{\rm{0}}{\rm{.0003 - 0}}{\rm{.0001i}}}&{{\rm{0}}{\rm{.0006 + 0}}{\rm{.0000i}}}\\ {{\rm{0}}{\rm{.0001 + 0}}{\rm{.0005i}}}&{{\rm{0}}{\rm{.9955 + 0}}{\rm{.0000i}}}&{{\rm{0}}{\rm{.0006 + 0}}{\rm{.0000i}}}&{{\rm{ - 0}}{\rm{.0002 - 0}}{\rm{.0001i}}} \end{array}}\right]\end{equation}
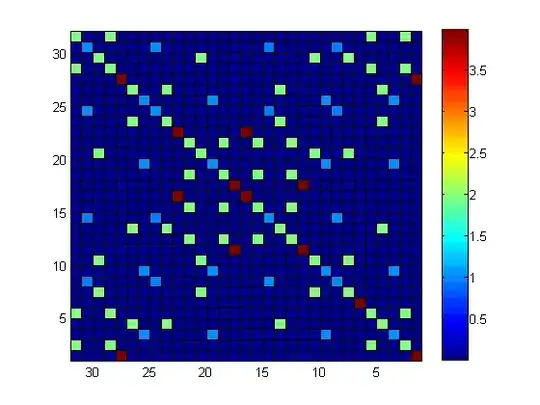
and the covariance matrix \begin{equation} V = E\left\{ {\left[ {\begin{array}{*{20}{c}} {{\mathop{\rm vec}\nolimits} \left( U \right)}\\ {{\mathop{\rm vec}\nolimits} \left( {\overline U } \right)} \end{array}} \right]{{\left[ {\begin{array}{*{20}{c}} {{\mathop{\rm vec}\nolimits} \left( U \right)}\\ {{\mathop{\rm vec}\nolimits} \left( {\overline U } \right)} \end{array}} \right]}^*}} \right\}\end{equation}
shown as the following figure (magnitude of the elements in $V$).