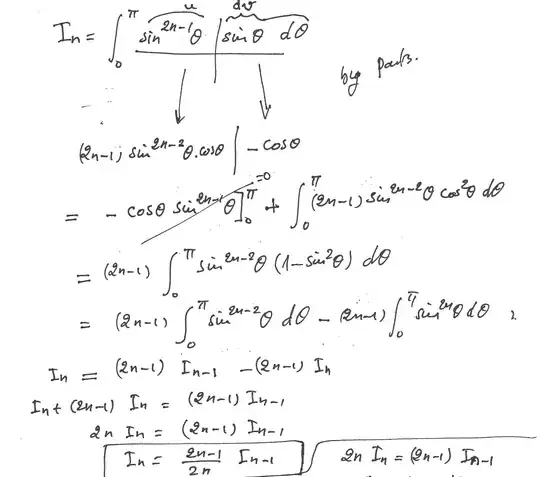
If $I_n=\int _0^{\pi }\:sin^{2n}\theta \:d\theta $, show that $I_n=\frac{\left(2n-1\right)}{2n}I_{n-1}$, and hence $I_n=\frac{\left(2n\right)!}{\left(2^nn!\right)2}\pi $
Hence calculate $\int _0^{\pi }\:\:sin^4tcos^6t\:dt$
I knew how to prove that $I_n=\frac{\left(2n-1\right)}{2n}I_{n-1}$ ,, but I am not very good at English, what does it mean Hence $I_n=\frac{\left(2n\right)!}{\left(2^nn!\right)2}\pi $ do we need to prove this part as well or is it just a hint to use? and for the other calculation to find $\int _0^{\pi }\:\:sin^4tcos^6t\:dt$ is there something in the first part that I can do to help me solve this question because otherwise it becomes very long and it's part of the question.