Here is a graph of the function $y=-1/x$:
If we add infinitely many similar functions with a shift of $\pi/2$ each in both directions, we get $\tan x$. But if we do the same only in one direction, we get "incomplete tangent":
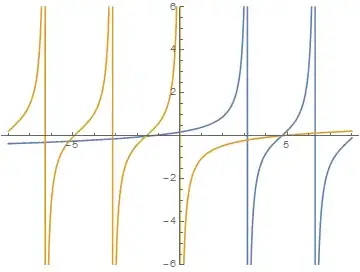
The yellow one is $\operatorname{pg}(x)=\frac 1\pi \psi (\frac x\pi)$, the blue one is $\operatorname{cpg}(x)=-\frac 1\pi \psi (1-\frac x\pi)$. They obey $\operatorname{cpg}(x)+\operatorname{pg}(x)=-\cot(x)$.
Now if we differentiate cpg(x) we get:
$$(\operatorname{cpg}(x))^{(s-1)}=\pi^{-s}\Gamma(s)\zeta(s,1-\frac x\pi)$$
At $x=0$ it would be
$$\operatorname{cpg}^{(s-1)}(0)=\pi^{-s}\Gamma(s)\zeta(s)$$
Compare it with this formula involving Riemann Xi-function:
$$\xi(2s) = \pi^{-s}\Gamma\left(s\right)\zeta(2s)$$
I wonder is the similarity between these two formulas just a coincidence or Riemann Xi function serves as a consecutive derivative (generating function) of some simple or notable function?
For example the function $\cot z=\frac{\sin'}{\sin}(x)$ has simple poles at $k\pi$ with residue $1$. The sum $f(z)=\frac1z+\sum_{k=1}^\infty\left(\frac1{z+k\pi}+\frac1{z-k\pi}\right)$ has the same property. It can be verified that difference is bounded and both functions are odd, so they are equal.
You can try the same for $\frac1{\sin z}$ or $\frac{\Gamma'}{\Gamma}$.
– G.Kós Nov 19 '14 at 07:47