4

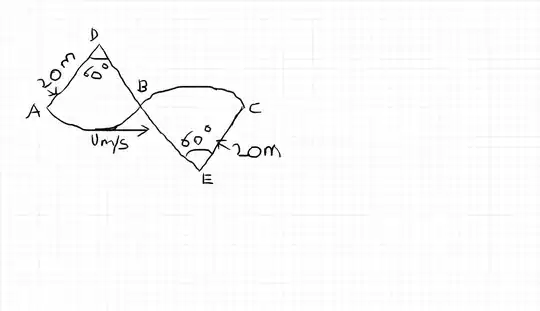
enter image description here

A toboggan travels along the path ABC shown in the diagram. The path lies in a vertical plane, and consists of two circular arcs $AB$ and $BC$. The line ABC is horizontal and there is no friction between the toboggan and the snow. Air resistance is negligible and the toboggan may be treated as a particle. The speed of the toboggan is at its lowest point is $U ms^{-1}$. Find the range of values of $U$ for which the toboggan will reach $C$ without losing contact with the snow.

I have absolutely no idea how to do this question. I spent about half an hour trying to figure out how to start. Finally did this: I found out the distance between the lowest point on the arc and the line AB and tried to equating the loss of gravitational potential energy with the gain on kinetic energy and used that to find the value of U as 7.32 (this was with the assumption that the speed of the particle as A was 0, which i'm pretty sure is a wrong assumption). Anyway, now i'm stuck and I have no idea what to do. Any help would be appreciated

user140161
  • 1,363

2 Answers2

0

At the point you have draw the kinetic energy is $E_k=\frac12 mU^2.$ If we assume that at this point the potential energy is zero, then $E=E_k+E_p=\frac12 mU^2,$ which is a constant, since there is no friction nor air resitance. Thus, at $B$ we have that $\frac12 mU^2=E=E_k+E_p=E_k+10mg.$ At the highest point that achieves the toboggan (necessary to go to $C$) it is $\frac12 mU^2=E=E_k+E_p=E_k+20mg.$ Since $E_k$ is nonnegative at such a point we get that $U^2\ge 40,$ that is, $U\ge 2\sqrt{10}m/s.$

mfl
  • 29,399
0

Let $r = 20$ be the radius, let $h$ be the height difference between the lowest point on arc $AB$ and the highest point on arc $BC$, and let $V$ be the speed at the highest point on arc $BC$. By drawing some right triangles and taking advantage of symmetry, we find that: $$ h = 2(r - r\sin 60^{\circ}) = (2 - \sqrt 3)r $$ By conservation of energy, we have: $$ \frac{1}{2}mU^2 = mgh + \frac{1}{2}mV^2 \iff V^2 = U^2 - 2gh $$ To barely reach $C$, we at least need that $V \geq 0$, so we can find our lower bound for $U$ as follows: $$ U^2 - 2gh \geq 0 \iff U \geq \sqrt{2gh} = \sqrt{2(9.8)(2 - \sqrt 3)(20)} = 10.2487\ldots $$

Now at the top of the arc $BC$, we have centripetal force: $$ mg - F_N = \frac{mV^2}{r} \iff V^2 = r(g - \tfrac{F_N}{m}) $$ To reach $C$ without losing contact with the snow, we need that $F_N \geq 0$, so we can find our upper bound for $U$ as follows: $$ U^2 - 2gh = V^2 = r(g - \tfrac{F_N}{m}) \leq rg - 0 \\\iff U \leq \sqrt{g(r + 2h)} = \sqrt{9.8(20 + 2(2 - \sqrt 3)(20))} = 17.3504\ldots $$ Thus, we conclude that: $$ 10.2487\ldots \leq U \leq 17.3504\ldots $$

Adriano
  • 41,576
  • That is an excellent answer. I have only recently started mechanics so could you also please share your motivation, briefly? I ask for that so that I get some sense about how to approach mechanics questions like these and know what lines to think along. – user140161 Nov 13 '14 at 22:34
  • 1
    I suppose it takes a bit of experience and intuition. Think about why there must be a lower bound for $U$: if we were going too slow, then we wouldn't make it all the way up the hill. Then think about why there must be an upper bound for $U$: if we were going too fast, then we might fly off the hill. The trick is then to turn these gut feelings into concrete constraints. – Adriano Nov 13 '14 at 22:46
  • I discussed this with my teacher today and found out that the method he proposed yielded different solutions. I got the same value for the lower bound of U but a different value (15.1) for the upper bound. He said that we form the centripetal force equation for the toboggan at point $B$ and not at the highest point on arc $BC$ as the particle is more likely to lose contact at this point than at the highest point of arc $BC$. This is left me slightly confused. Which is the correct method? – user140161 Nov 17 '14 at 15:37