2

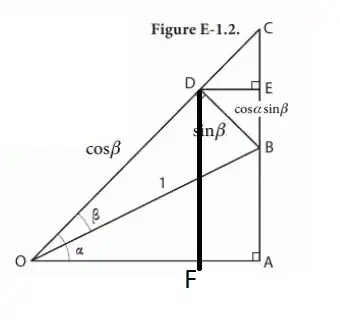
I can't solve the following problem (From the book: The Forgotten Art of Spherical Trigonometry):

enter image description here

I can't manage to prov it geometrically.

I could get that I have to find AB and the values indicated in the diagram. I also think that D angle in DCE is equal to alpha as B in BED is, making DCE and BED similar, but then I always get very complicated calculation when I try to give a dimension to CE or DC.

How it is the smart way?

Thanks

sylvester
  • 227

3 Answers3

0

Hint: Sine is an odd function so $$\sin(-\beta) = -\sin(\beta)$$

graydad
  • 14,077
  • I think the question looks for the geometric solution (b). You gave the correct way to solve (a). – John Nov 12 '14 at 23:44
0

enter image description here

$$AB = DF - BE $$

where:

$AB = OB\sin(\alpha - \beta) = \sin(\alpha - \beta)$

$DF = OD\sin \alpha = \cos\beta\sin\alpha$

$BE = BD\cos \alpha = \sin\beta\cos\alpha$

Petite Etincelle
  • 14,767
0

Since $DEAO$ is a parallelogram, $\angle CDE = \alpha$.

Since $\angle DEB$ is a right angle, $\angle EBD = \alpha.$

From there you can calculate $CD, DE, CE$.

Then, by writing down $CA = CE + EB + BA,$

$$\sin \alpha (\cos \beta + \tan \alpha \sin \beta) = \sin \alpha \tan \alpha \sin \beta + \cos \alpha \sin \beta + \sin(\alpha - \beta),$$

the result follows by algebra.

John
  • 26,319