As a follow-up to a previous question, I'd like to know if
$$\sum_{n=1}^\infty\frac{1}{2 ^ n}$$
is convergent? If yes, then what does it converge to?
Just as a sidenote - the whole issue started with reading about Zeno's Turtle Paradox which made me curious about the underlying mathematics.
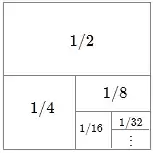
This series is a geometric series and converges, see the link in the comments.
But, I'll offer the standard proof that this particular series converges here:
A series is defined to converge to $L$ if and only if the sequence of its partial sums converges to $L$:
The infinite series $ \sum\limits_{n=1}^\infty a_n$ converges to $L$ if and only if the sequence of partial sums $\{S_n\}$, defined by $$S_n=\sum\limits_{m=1}^n a_m =a_1+a_2+a_3+\cdots+a_n,$$ converges to $L$.
If you consider the sum of the first $n$ terms, $S_n$, for $\sum\limits_{n=1}^\infty {1\over 2^n}$, then $$S_n=\sum\limits_{m=1}^n{1\over2^m}.$$ Writing out this sum explicitly gives $$ S_n={1\over 2}+{1\over 2^2}+\cdots+{1\over 2^n}. $$ Multiply both sides of the above by $1\over2$: $$ {1\over 2} S_n = {1\over 2^2}+{1\over 2^3}+\cdots+{1\over 2^{n+1}} $$ Now add $1\over2$ to both sides: $$ {1\over 2} S_n+{1\over2} =\underbrace{{1\over 2}+ {1\over 2^2}+{1\over 2^3}+\cdots+ +{1\over 2^n}}_{S_n}+{1\over 2^{n+1}} $$ Then: $$ {1\over 2} S_n+{1\over2} =S_n+{1\over 2^{n+1}}. $$ Solving the above for $S_n$ gives: $$ {1\over2}-{1\over 2^{n+1}}={1\over2}S_n $$ $$ S_n=1-{1\over 2^n}. $$ From the above, we can see that as $n\rightarrow\infty$, $S_n\rightarrow1$. So $\sum\limits_{n=1}^\infty {1\over 2^n}=1$.
