Calculating line integrals via Stokes theorem

Question

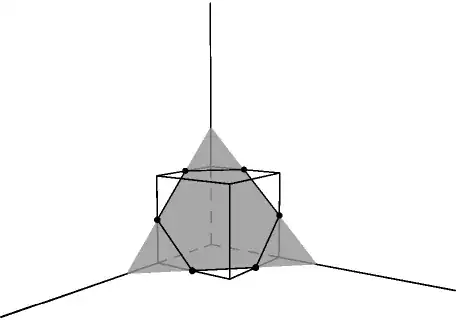
(a)Evaluate the integral

$$\int_{C}(y^2-z^2)\:dx+(z^2-x^2)\:dy+(x^2-y^2)\:dz$$

The curve C is the intersection of the boundary surface of the cube $0 ≤ x, y, z ≤ a,$ with the plane $x+y +z = 3a/2$

What i tried

For part (a)I would think of using stokes theorem and i would first calculate $curl F$ which gives $<-2y-2z,2z-2x,-2x-2y>$ while i would calculate the normal n to be $<1,1,1>$ then do a dot product between $curl F$ and $n$ to get $<-4y-4x-4z>$ and substituting $z=3a/2-x-y$. I know that i would need to parametrise this $F$ in order to get the normal $$\iint\!-6a\,dS $$

The etiquette requires a new question for (b): http://meta.math.stackexchange.com/questions/2814/edit-and-rephrase-or-ask-new-question. — Martín-Blas Pérez Pinilla, Nov 13 '14 at 10:56
I posted the link for the other question. http://math.stackexchange.com/questions/1020136/calculating-line-integrals-using-stokes-theorem-vector-calculus — ys wong, Nov 13 '14 at 14:56

Martín-Blas Pérez Pinilla · Accepted Answer · 2014-11-19T10:16:01.500

2

The surface is a regular hexagon with vertices $(a,a/2,0)$, $(a/2,a,0)$, $(a,0,a/2)$, $(a/2,0,a)$, $(0,a,a/2)$, $(0,a/2,a)$ (intersections of plane $x+y+z=3a/2$ with the edges of cube). Let be $D$ the projection on the plane XY, another hexagon with vertices $(a,a/2)$, $(a/2,a)$, $(a,0)$, $(a/2,0)$, $(0,a)$, $(0,a/2)$. Then the surface will be $$x=x$$ $$y=y$$ $$z=3a/2−x−y$$ $$(x,y)\in D.$$ The normal vector is $N=(1,0,-1)\times(0,1,-1)=(1,1,1)$. The surface integral is $$\iint_D{\text{curl}}F\cdot N\,dxdy = \iint_D-6a\,dxdy = -6a\,\text{area}(D)=-\frac92a^3.$$

EDIT:

Integration limits for $D$: $$\int_0^{a/2}\int_{a/2-x}^adydx+\int_{a/2}^a\int_0^{3a/2-x}dydx$$ Parametrization of the curve: take two consecutive vertices, for example, $(a,a/2,0)$, $(a/2,a,0)$. The parametrization of this segment is easy: $$(x,y,z)=(a,a/2,0)+((a/2,a,0)-(a,a/2,0))t,\qquad t\in[0,1].$$ Do the same with the other five edges. Warning: the orientation of each segment is important.

EDIT 2: added a drawing.

Intersection plane-cube

edited Nov 19 '14 at 10:16

answered Nov 12 '14 at 08:53

Martín-Blas Pérez Pinilla

41,546
4
46
89

I got a normal of $<1,1,1>$ and then i do a dot product with $curlF$, how do i then proceed from here, im stuck at the integration limits. – ys wong Nov 12 '14 at 11:33
1

@yswong, you need know the vertices of $D$, but the integration limits are unnecessary. The surface integral is simply $-6a\text{area}(D)$. – Martín-Blas Pérez Pinilla Nov 12 '14 at 11:42
Yup im having problems finding the area of D, i managed to get -6a but for area(D) i got $(9/4)a^2$ which i dont think is right. – ys wong Nov 12 '14 at 13:05
@yswong, in your calculations, what vertices has $D$? – Martín-Blas Pérez Pinilla Nov 12 '14 at 14:03
My vertices are $(3a/2,0,0)$ ,$(0,3a/2,0)$ and $(0,0,3a/2)$ and $D$ is a parallelogram. What i did was to find lengths of the sides of the parallelogram and then multiplying them – ys wong Nov 12 '14 at 14:34
Wrong! The surface is a regular hexagon and $D$ is another hexagon. Tomorrow, I will expand my answer if you haven't finished. – Martín-Blas Pérez Pinilla Nov 12 '14 at 14:54
Could u explain this to me please, beacuse im unsure about this part. Thanks – ys wong Nov 12 '14 at 15:09
Oh thanks, i think i got it. – ys wong Nov 13 '14 at 09:07
Let us continue this discussion in chat. – ys wong Nov 13 '14 at 10:25

Calculating line integrals via Stokes theorem

1 Answers1

Linked