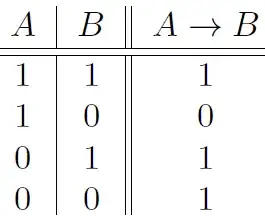
In logic, do the $\Longrightarrow$ and $\rightarrow$ signify different things?

Question

In logic, do the $\Longrightarrow$ and $\rightarrow$ signify different things? Are there contexts where one is more appropriate than the other?

I had believed that the $\Longrightarrow$ was for metalogic, and the $\rightarrow$ was for logic. However, recently, I've noticed $\Longrightarrow$ used more often than $\rightarrow$ in non-metalogical logical contexts.

Usually $\implies$ is metalinguistic. I've never seen it used as part of the language, but I've heard it some times is. — Git Gud, Nov 10 '14 at 19:04
http://math.stackexchange.com/questions/630391/what-does-rightarrow-mean-in-p-rightarrow-q — Asaf Karagila, Nov 10 '14 at 19:17
http://math.stackexchange.com/questions/68932/whats-the-difference-between-material-implication-and-logical-implication — Asaf Karagila, Nov 10 '14 at 19:19
I'll add to Asaf Karagila's links that A. N. Prior's textbook Formal Logic has parts of it which read like the following: "Rule: Detachment ($\alpha$, D$\alpha$D$\beta$$\gamma$ $\rightarrow$ $\gamma$) and (In all cases the sole rule beside substitution is E-detachment: $\alpha$, E$\alpha$$\beta$ $\rightarrow$ $\beta$. And in my opinion Prior's symbolism comes as clearer here than writing {E$\alpha$$\beta$, $\alpha$} $\vdash$ $\beta$, since the "$\rightarrow$" symbol suggests that one transitions from the left-hand side to the right hand side. — Doug Spoonwood, Nov 10 '14 at 19:25
@GitGud I think it maybe dependent on country/books. For most o my education I've seen and written ⟹. I have come across → when I started to work with English books. — Trismegistos, Nov 10 '14 at 20:00
Does this answer your question? What's the difference between material implication and logical implication? — user1147844, Feb 23 '23 at 00:26

score 8 · Accepted Answer · answered Nov 10 '14 at 19:58

8

Long story short, $\rightarrow$ is a logic operator, whereas $\implies$ is a statement (where you know the outcome must be true).

$\rightarrow$ : can have result "false". $\\$ $\implies$ : Always true, by definition cannot be false. Not used as an operator.

answered Nov 10 '14 at 19:58

Protawn

562

3

Statements are easily false. $0=1$ is a statement which is demonstrably false in the natural numbers (assuming the consistency of Peano axioms, anyway). Moreover $\psi\rightarrow\varphi$ is a tautology if and only if $\psi\implies\varphi$ when talking about classical propositional calculus. – Asaf Karagila Nov 10 '14 at 20:17
@AsafKaragila: How do you prove falseness of $0=1$ and in particular why does it rely on the consistency of the Peano axioms? Can't you show $\neg(0=1)$ in any case? Or does it mean more than showing this when you say "demonstrably false". – Nikolaj-K Feb 11 '15 at 14:01
1

@Nikolaj: Those are just two constant symbols, nothing more. In a structure which interprets them as the same object, e.g. a singleton, they are equal. Assuming $\sf PA$ is consistent ensures that $\sf PA$ does not prove $0=1$ since it proves the negation of that statement. – Asaf Karagila Feb 11 '15 at 14:06

emcor · Answer 2 · 2014-11-10T19:28:38.443

5

The logical definition for "$A\to B$" is equivalent to $\neg A\vee B$:

enter image description here

"$A\Rightarrow B$" is hereby defined as an $A\to B$ which is always true (tautology).

E.g. "$n>4\to n>2$" is always true, hence it holds "$n>4\Rightarrow n>2$".

The converse does not hold: "$n>2\to n>4$" is an eligible statement, but "$n>2\Rightarrow n>4$" does not hold.

edited Nov 10 '14 at 19:28

answered Nov 10 '14 at 19:13

emcor

792

I can't think of any mathematical statements for which $\rightarrow$ is true, but $\longrightarrow$ is not. Could you give me an example? – Hal Nov 10 '14 at 19:57
3

Using the last example given by emcor, consider "$1>2\to 1>4$" is a valid and true statement since the premise is false, but "$1>2\implies 1>4$" is not a valid implication from a mathematical standpoint. – Cure Nov 10 '14 at 20:07
Since you define the single line arrow as not being the regular logical implication (A therefore B) but a statement, then what are the use and usefulness of statements like "A→B". Do you have an example? – mins Nov 07 '23 at 17:12

GFauxPas · Answer 3 · 2015-02-11T13:54:47.963

From what I've seen, $\longrightarrow$ and $\implies$ mean material implication, "if then". $\vdash$ and $\therefore$ are used for logical implication. $\implies$ seems to be more common in modern books and $\longrightarrow$ seems to be more common in older books.

Thus $p \implies q$ means that p is a sufficient condition for q and is false precisely when $\neg p \land q$. $p \vdash q$ means q follows from p by axioms, definitions, and theorems.

In logic, do the $\Longrightarrow$ and $\rightarrow$ signify different things?

3 Answers3

Linked