Can someone explain what exactly the Jacobian matrix is (specifically in its application to dynamical systems) and maybe give an example of how to compute it? It really confuses me...and I haven't been able to find any good resources online.
-
4Have a look at this link to start with: http://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant Does it make sense to you? – Avitus Nov 10 '14 at 16:16
1 Answers
For an answer to your question, review the answers to the MSE posting: What is Jacobian Matrix?.
As a practical dynamical systems example, lets look at a system from another problem you posed, we have:
$$f_1 = x'=y+x(1-x^2-y^2)$$ $$f_2 = y'=-x+y(1-x^2-y^2)$$
If we find the critical points for this system, we arrive at:
$$(x, y) = (0,0)$$
We can find the Jacobian matrix of this system as:
$$J_{(x,y)}(f)=\begin{pmatrix} \frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} \\ \frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} \end{pmatrix} = \begin{pmatrix} 1-3x^2-y^2 & 1 - 2 xy \\ -1 -2 xy & 1-x^2-3y^2 \end{pmatrix}$$
We can now evaluate the Jacobian at each critical point we found and look at the eigenvalues, arriving at:
$$J_{(0,0)}(f)=\begin{pmatrix} 1& 1 \\ -1 & 1 \end{pmatrix}$$
The eigenvalues are:
$$\lambda_{1,2} = 1 ~\pm ~i$$
This linearization tells us we have an unstable spiral.
A phase portrait shows (and verifies the linearization):
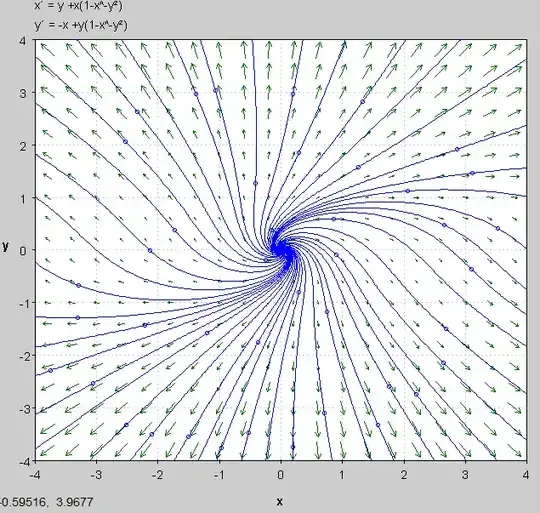
Note: It is important to note that this process only works for robust cases and not for marginal cases!