Analysis of the function $\prod_{n=-\infty}^{ \infty }(1-e^{-a{(x+n)^2} })$

Question

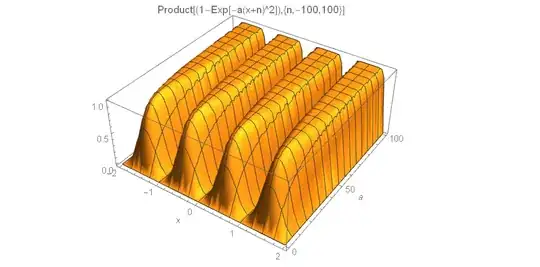
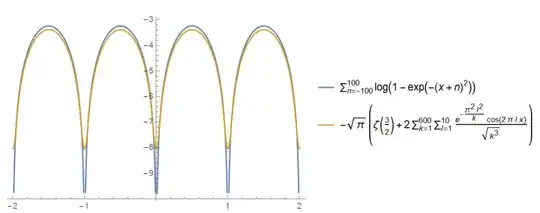
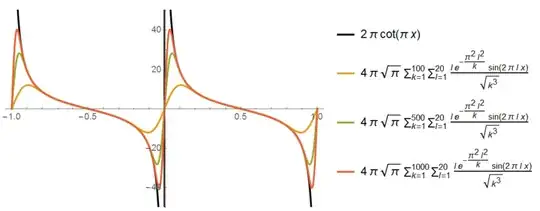
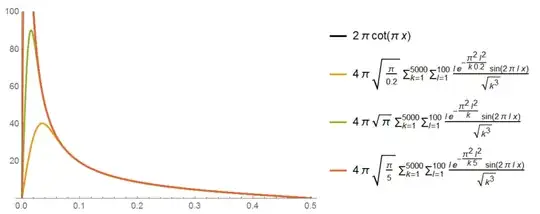
While playing on pruduct series, I noticed interesting function that it has similar behavior to $C\cdot\sin^2(\pi x)$ function . I need help about some results below.

$$f(x)=\prod\limits_{n=-\infty}^{ \infty }(1-e^{-a{(x+n)^2}}) $$ where $a>0$

The function is a periodic function because

$$f(x+1)=\prod\limits_{n=-\infty}^{ \infty }(1-e^{-a{(x+1+n)^2}}) =\prod\limits_{n=-\infty}^{ \infty }(1-e^{-a{(x+n)^2}}) $$

Some properties of the function:

---

• $f(x+1)=f(x)$ Period is $1$
• It is obvious that $f(k)=0$ where $k$ is integer.
• It is even function. $f(-x)=f(x)$

These properties above are same as $C.\sin^2(\pi x)$

My ideas and my aim to find out about the function are

1. Can we express it as known functions?
2. How closed form of $f(\frac{1}{2})$ can be found? I believe that the function behaves the same as $C\sin^2(\pi x)$ has and $f'(\frac{1}{2})=0$ but I could not prove it.
3. If it is a periodic function, what is the Fourier series expansion of the function?

Any reference links about the function and help will be appreciated very much .

Thanks

UPDATE: I proved my conjecture above , $f'(\frac{1}{2})=0$

I added some extra information too

$$\frac{f'(x)}{f(x)}=2a\sum\limits_{n=-\infty}^{ \infty } \frac{x+n}{e^{a{(x+n)^2}}-1} $$

$$\frac{f'(\frac{1}{2})}{f(\frac{1}{2})}=2a\sum\limits_{n=-\infty}^{ \infty } \frac{\frac{1}{2}+n}{e^{a{(\frac{1}{2}+n)^2}}-1} $$

$$\frac{f'(\frac{1}{2})}{f(\frac{1}{2})}=a\sum\limits_{n=-\infty}^{ \infty } \frac{2n+1}{e^{a{(\frac{1}{2}+n)^2}}-1}$$

$$f'(\frac{1}{2})=af(\frac{1}{2})\sum\limits_{n=-\infty}^{ \infty } \frac{2n+1}{e^{a{(\frac{1}{2}+n)^2}}-1}$$

$$f'(\frac{1}{2})=af(\frac{1}{2})\sum\limits_{n=-\infty}^{ -1 } \frac{2n+1}{e^{a{(\frac{1}{2}+n)^2}}-1}+af(\frac{1}{2})\sum\limits_{n=0}^{ \infty } \frac{2n+1}{e^{a{(\frac{1}{2}+n)^2}}-1}$$

$$f'(\frac{1}{2})=af(\frac{1}{2})\sum\limits_{k=0}^{ \infty } \frac{-(2k+1)}{e^{a{(-1)^2(\frac{1}{2}+k)^2}}-1}+af(\frac{1}{2})\sum\limits_{n=0}^{ \infty } \frac{2n+1}{e^{a{(\frac{1}{2}+n)^2}}-1}$$

$$f'(\frac{1}{2})=-af(\frac{1}{2})\sum\limits_{k=0}^{ \infty } \frac{2k+1}{e^{a{(\frac{1}{2}+k)^2}}-1}+af(\frac{1}{2})\sum\limits_{n=0}^{ \infty } \frac{2n+1}{e^{a{(\frac{1}{2}+n)^2}}-1}$$

$$f'(\frac{1}{2})=0$$

There can be proved in same way that

$f'(\frac{2k+1}{2})=0$ where $k$ is integer.

UPDATE: Nov 13th

I tried to used roots of $1-e^{-a{(x+n)^2}}$ . I would like to share my results. Maybe it can be helpful to find out an expression with known functions.

$$1-e^{-a{(x+n)^2}}=0$$ roots are:

$$a{(x+n)^2}=2k\pi i$$ Where $k$ integer.

If $k=0$

Roots $x=-n$ where $n$ is integer as known. for $k=0$ and They are double roots ,Thus

$$\prod\limits_{n=-\infty}^{ \infty }1-e^{-a{(x+n)^2}}=x^2\prod\limits_{n=1}^{ \infty }(1-\frac{x^2}{n^2})^2\prod\limits_{n=-\infty}^{ \infty }G(x,a)$$

$$f(x)=\frac{\sin^2 (\pi x)}{\pi^2}\prod\limits_{n=-\infty}^{ \infty }G(x,a)$$

$\prod\limits_{n=-\infty}^{ \infty }G(x,a)$ will be expressed by other roots for $k\neq 0$

$$\prod\limits_{n=-\infty}^{ \infty }G(x,a)=\prod\limits_{n=-\infty}^{ \infty }\prod\limits_{k=1}^{ \infty }(1-\frac{x}{-n+\sqrt{\frac{2k \pi i }{a}}})(1-\frac{x}{-n-\sqrt{\frac{2k \pi i }{a}}})(1-\frac{x}{-n+\sqrt{\frac{-2k \pi i }{a}}})(1-\frac{x}{-n-\sqrt{\frac{-2k \pi i }{a}}})$$

$$\prod\limits_{n=-\infty}^{ \infty }G(x,a)=\prod\limits_{n=-\infty}^{ \infty }\prod\limits_{k=1}^{ \infty }(1+\frac{2nx}{n^2-\frac{2k \pi i }{a}}+\frac{x^2}{n^2-\frac{2k \pi i }{a}})(1+\frac{2nx}{n^2+\frac{2k \pi i }{a}}+\frac{x^2}{n^2+\frac{2k \pi i }{a}})$$

$$\prod\limits_{n=-\infty}^{ \infty }G(x,a)=\prod\limits_{n=-\infty}^{ \infty }\prod\limits_{k=1}^{ \infty }(\frac{(x+n)^2-\frac{2k \pi i }{a}}{n^2-\frac{2k \pi i }{a}})(\frac{(x+n)^2+\frac{2k \pi i }{a}}{n^2+\frac{2k \pi i }{a}})$$

So finally we can write ;

$$f(x)=\frac{\sin^2 (\pi x)}{\pi^2}\prod\limits_{n=-\infty}^{ \infty }\prod\limits_{k=1}^{ \infty }(\frac{(x+n)^4+\frac{4\pi^2 k^2 }{a^2}}{n^4+\frac{4 \pi^2 k^2 }{a^2}})$$

I thought to change product order can help us, so to get

$$f(x)=\frac{\sin^2 (\pi x)}{\pi^2}\prod\limits_{k=1}^{ \infty }\prod\limits_{n=-\infty}^{ \infty }(\frac{(x+n)^4+\frac{4\pi^2 k^2 }{a^2}}{n^4+\frac{4 \pi^2 k^2 }{a^2}})$$

I am till here for now, But I do not see how to go from here to get a nice expression with known functions.

Thanks for helps

EDIT: 1/9/2017

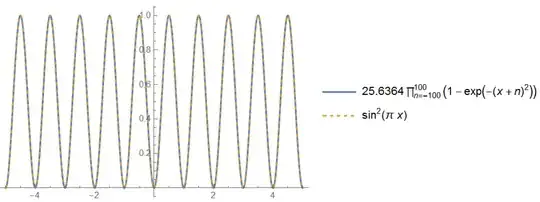
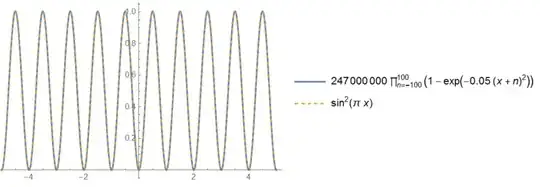
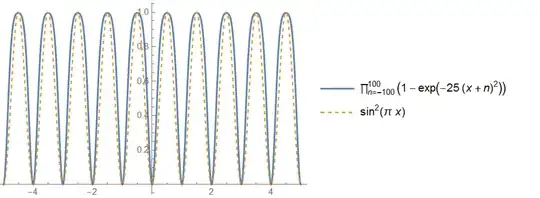
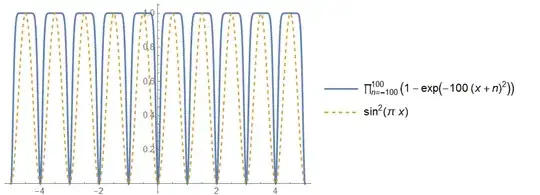
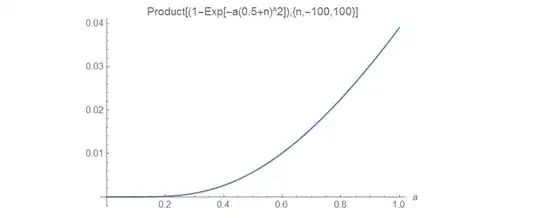
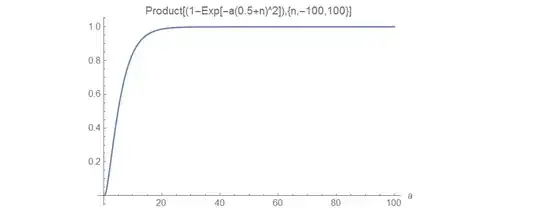
After @Yuriy S 's wonderful graphics, I realized that we may express the $f(x,a)$ in approximation.

$$f(x,a)=\prod\limits_{n=-\infty}^{ \infty }(1-e^{-a{(x+n)^2}}) $$ where $a>0$

Known values of $f(x,a)$:

1. $f(x,0)=0$
2. $\lim_{a\to\infty} f(x,a)=1$
3. $f(1/2+k,a)$ has maximum, where $k$ is integer
4. $f(k,a)=0$, where $k$ is integer
5. $f(x,a)$ is periodic function over $x$

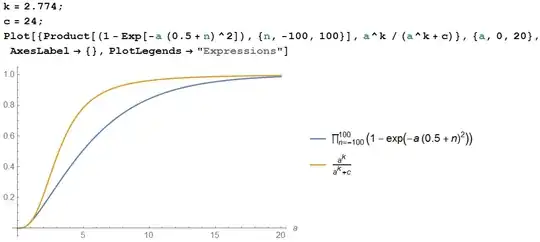
I conjecture that $f(x,a) \approx \cfrac{a^k \sin^2(\pi x)}{a^k \sin^2(\pi x)+c}$ ,where $a>0$, $k,c$ are positive real numbers,

From Graphics below, I calculated $k$ and $c$.

in sixth graph,

$$f(1/2,1)\approx 0.04$$ $$f(1/2,0.6)\approx 0.01$$

From these results, I got $k$ and $c$.

$k \approx 2.774$ and $c \approx 24$.

Maybe someone can help me to calculate $k$ and $c$ more accurately.

Thanks Best Regards

Answer 1

It's not an answer, but there are a lot of graphs which can't be put into a comment.

The function $\prod\limits_{n=-\infty}^{ \infty }(1-e^{-a{(x+n)^2}})$ is very close to $C \sin^2(\pi x)$ for $a \leq 1$, as can be seen by numerical experiments:

1) For $a=1$ the scaling constant $C=0.0390070548953618...$ and the functions are practically indistinguishable.

2) For $a<<1$ the functions are also very close with appropriate scaling.

3) However, for $a>>1$ the functions are different, since $f(x)$ approaches a constant around its maxima.

---

The overall $a$ dependence can be seen in the following 3D graph and the $f(1/2)$ graphs for the dependence around a maximum. The latter has the character of a logistic function.

---

I didn't have much luck with analytics so far, but I will expand my post into a proper answer if something useful comes up.

---

Update. As asked by the OP, I tested their approximation, it's not very good:

Answer 2

I post this answer separately, so that the analytics are not lost among the illustrative material from my first post.

This answer deals with Fourier series, not for the function $f(x)$ itself, but for its logarithm.

It's often easier to deal with the logarithms of infinite products, since they are represented as infinite series.

$$\ln f(x)=\sum_{n=-\infty}^\infty \ln(1-e^{-a{(x+n)^2}})=$$

Since $a(x+n)^2>0$ we can always expand the logarithm into its Taylor series:

$$=-\sum_{n=-\infty}^\infty \sum_{k=1}^\infty \frac{1}{k} e^{-ka(x+n)^2}=-\sum_{k=1}^\infty \frac{1}{k} e^{-kax^2} \sum_{n=-\infty}^\infty e^{-kan(n+2x)}$$

The latter sum fits the definition of a Jacobi Theta Function $\vartheta_3$, thus:

$$\sum_{n=-\infty}^\infty e^{-kan(n+2x)}=\sqrt{\frac{\pi}{ka}} e^{kax^2} \vartheta_3 \left(\pi x, e^{-\frac{\pi^2}{ka}}\right)$$

This result is confirmed by Wolfram Alpha.

This looks complicated, but there is another series representation for $\vartheta_3$ which might help:

$$\vartheta_3 \left(\pi x, e^{-\frac{\pi^2}{ka}}\right)=1+2\sum_{l=1}^\infty e^{-\frac{\pi^2l^2}{ka}} \cos(2 \pi l x)$$

Now we obtain:

$$\ln f(x)=-\sqrt{\frac{\pi}{a}} \sum_{k=1}^\infty \frac{1}{k^{3/2}} \left(1+2\sum_{l=1}^\infty e^{-\frac{\pi^2l^2}{ka}} \cos(2 \pi l x) \right)$$

And finally:

$$\ln f(x)=-\sqrt{\frac{\pi}{a}} \zeta \left( \frac32 \right) -2\sqrt{\frac{\pi}{a}} \sum_{l=1}^\infty \sum_{k=1}^\infty \frac{1}{k^{3/2}} e^{-\pi^2l^2/(ka)} \cos(2 \pi l x)$$

Or, introducing:

$$C_l (a)=\sum_{k=1}^\infty \frac{1}{k^{3/2}} e^{-\pi^2l^2/(ka)}$$

The familiar form of a Fourier series emerges (with the first term being the constant term $l=0$):

$$\ln f(x)=-\sqrt{\frac{\pi}{a}} \zeta \left( \frac32 \right) -2\sqrt{\frac{\pi}{a}} \sum_{l=1}^\infty C_l (a) \cos(2 \pi l x)$$

The convergence is not very good, however the $l$ sum converges much faster than the $k$ sum (which should be obvious by looking at the exponential term in $C_l$). Thus, we don't need a lot of Fourier terms, but the coefficients have to be computed precisely.

Here is an illustration for $a=1$:

---

This Fourier series allows us excellent insight into similarities with the $C \sin^2 (\pi x)$ function.

$$\frac{(\sin^2 (\pi x))'}{\sin^2 (\pi x)}=2 \pi \cot (\pi x)$$

$$\frac{f'(x)}{f(x)}=(\ln f(x))'=4 \pi \sqrt{\frac{\pi}{a}} \sum_{l=1}^\infty l~C_l \sin(2 \pi l x)$$

It turns out, these new functions are very close for $a=1$ (if we compute $C_l$ accurately enough):

However, there is a correlation - the larger $a$, the faster $k$-sum converges, but the slower $l$-sum converges. Thus, if $a$ is small you need to take more terms in $k$-sum, but if $a$ is large you ned to take more terms in the $l$-sum.

Here are plots for the same large number of terms for $a=0.2,1,5$:

---

Disclaimer

The Fourier series has been introduced in this answer, I have not seen it before writing my own, even though it's linked above in the comments to the OP. I acknowledge that Semiclassical got there first.