My (divergent) summation of the zetas with sets of cofactors give systematically errors of simple integer differences. What am I missing?

Question

This is a "fiddling" in a small project of mine with which I'm concerned from time to time for three years now. I try to focus on the core of the problem, please ask if more context is needed.

---

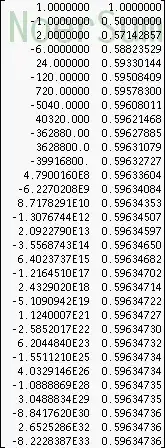
Consider the divergent series $$ \sum_{k=1}^\infty {(-1)^{k-1} \over k }\zeta(-k) \underset{\mathcal N}{=} s_1 = -0.081061466... $$ Here the symbol "$\underset{\mathcal N}{=} $" means, that I did that sum by the Noerlund-summation-method using 64 terms. The value which I expect by some other derivation which I'll explain below is $ -\zeta(0)' = 0.91893853 $ which differs exactly by 1.

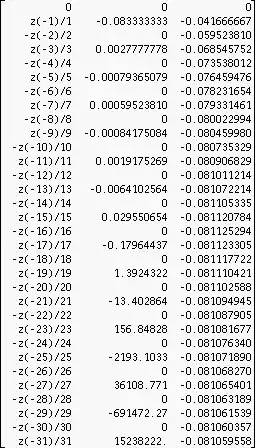
More context: the coefficients at the zetas are taken just from the matrix of Stirling-numbers of the first kind, denote them simply as $s1_{r,c}$ , so the defition stems really from: $$ \sum_{r=1}^\infty s1_{r,1} \cdot {1! \over r! }\zeta(-r) \underset{\mathcal N}{=} s_1 $$

---

Next consider the divergent series taken from the next column in the Stirling matrix: $$ \sum_{k=1}^\infty s1_{k,2} \cdot { 2! \over k! }\zeta(-k) \underset{\mathcal N}{=} s_2 = -0.006356455... $$ The value which I expect by the other derivation is $ \zeta(0)'' = -2.00635645591... $ which differs (relatively near) by $2!$. (The difference can be made smaller by taking more terms for the Noerlund-summation)

---

To make things short, I'm doing the dotproduct $$ Z \cdot S1 \underset{\mathcal N}{=} Y $$ where the infinite rowvector $Z$ contains the consecutive zetas $\zeta(0),\zeta(-1),\zeta(-2), ...$ and $S1$ is the matrix containing the Stirlingnumbers first kind, scaled by factorials such that $$ S1_{r,c} = s1_{r,c} \cdot { c!\over r!} $$ getting the result-vector $Y$ which deviates from my expected result of derivatives $ \zeta(0)^{(c)}$ by factorials such that $$ Y[c]= (-1)^c \cdot (\zeta(0)^{(c)} + c!) $$

---

The problem is connected with that of the Ramanujan-summation of the series of like powers of logarithms: $$ \sum_{k=0}^{\infty} \log(1+k)^c \underset{\mathcal Z}{=} (-1)^c \cdot \zeta(0)^{(c)} $$ where I get (by "$\mathcal Z $" eta-regularization) the "magic constants" having the same values as I described above and which deviate by the expected values for that sums (by the signed $\zeta(0)$-derivatives) exactly the factorials. (See my earlier question in MSE but in which I had not yet that more general view with the columns of the Stirlingmatrix)

Additional remarks: the complete background can be found in this article (I'm just editing the concerning paragraphs) and was remotivated by the recent question here in MSE

Answer 1

Here is my ongoing, partial solution:

Problem

The major issue is that the sum

$$ A_{k} := \sum_{n=1}^{\infty} \frac{S_{n,k}}{n!} \zeta(-n) \tag{1} $$

is not Abel-summable, hence not Nørlund-summable, where $S_{n,k}$ is the Stirling number of the 1st kind. (Note that any Nørlund-summable series for any choice of weight is also Abel-summable and has the same value.) This is because the non-zero terms of the series (1) have approximately factorial growth. (Indeed, accepting some asymptotic relations for $S_{n,k}$ then the non-zero terms satisfy

$$ \frac{S_{2n-1,k}}{(2n-1)!}\zeta(1-2n) \sim (-1)^{n-k-1} \frac{2\gamma_{1}}{(k-1)!} \frac{(2n-1)! \log^{k-1} n}{(2\pi)^{n}}, $$

see this paper.) So we instead consider the following regularization:

Definition. For any sequence $(\lambda_{n})$ satisfying $\lambda_{n}/\log (n!) \to \infty$ as $n\to\infty$, we define $$ A_{k}(r) = \sum_{n=1}^{\infty} \frac{S_{n,k}}{n!} \zeta(-n) e^{-\lambda_{n} r}. $$

(To be pedantic, we should also demonstrate the dependence on the choice of $(\lambda_{n})$. But we choose more practical point of view instead.) According to the estimation above, we find that $A_{k}(r)$ defines an analytic function for $\Re(r) > 0$.

Unfortunately, not any choice of $(\lambda_{n})$ allows regularization. Indeed, for $\lambda_{n} = 2^{n}$, the High Indice Theorem tells us that $A_{k}(0^{+})$ does not exist. Thus the best thing we can hope is:

Goal. Find a suitable sequence $(\lambda_{n})$ such that $A_{k} := A_{k}(0^{+})$ exists and is equal to $$ k!A_{k} = (-1)^{k}(\zeta^{(k)}(0) + k!). \tag{2} $$

Main Calculation

Step 1. For $|s| < 1$, we consider the sum

$$ B(r, s) = \sum_{k=0}^{\infty} A_{k}(r)s^{k}. $$

Then by the property of $S_{n,k}$, we have

\begin{align*} B(r, s) &= \sum_{k=0}^{\infty} \sum_{n=1}^{\infty} \frac{S_{n,k}}{n!} \zeta(-n)e^{-\lambda_{n} r}s^{k} = \sum_{n=1}^{\infty} \frac{\zeta(-n)}{n!} e^{-\lambda_{n} r} \left( \sum_{k=0}^{\infty} S_{n,k}s^{k} \right) \\ &= \sum_{n=1}^{\infty} \frac{s!}{(s-n)!n!} \zeta(-n) e^{-\lambda_{n} r} = \sum_{n=1}^{\infty} \binom{s}{n} \zeta(-n) e^{-\lambda_{n} r}. \tag{3} \end{align*}

Here, interchanging the order of summation is justified by Fubini's Theorem, together with the following estimate:

\begin{align*} \sum_{k=0}^{\infty} \sum_{n=1}^{\infty} \left| \frac{S_{n,k}}{n!} \zeta(-n)e^{-\lambda_{n} r}s^{k} \right| &= \sum_{n=1}^{\infty} \frac{|\zeta(-n)|}{n!} e^{-\lambda_{n} \Re r} \left( \sum_{k=0}^{\infty} |S_{n,k}| |s|^{k} \right) \\ &\lesssim \sum_{n=1}^{\infty} \frac{\Gamma(|s|+n)}{\Gamma(|s|)} e^{-\lambda_{n} \Re r} < \infty. \end{align*}

Step 2. Now using the (asymmetric) functional equation of the Riemann zeta function, for $n \geq 1$ we get

\begin{align*} \zeta(-n) &= \frac{1}{\pi} (2\pi)^{-n} \sin\left(-\frac{\pi n}{2}\right) \Gamma(n+1)\zeta(n+1) \\ &= \frac{1}{\pi} \int_{0}^{\infty} \frac{(-it/2\pi)^{n} - (it/2\pi)^{n}}{2i} \frac{dt}{e^{t} - 1} \\ &= 2 \int_{0}^{\infty} \frac{(-it)^{n} - (it)^{n}}{2i} \frac{dt}{e^{2\pi t} - 1}. \end{align*}

Plugging this back to (3) gives

$$ B(r, s) = 2 \sum_{n=1}^{\infty} \binom{s}{n} e^{-\lambda_{n} r} \int_{0}^{\infty} \frac{(-it)^{n} - (it)^{n}}{2i} \frac{dt}{e^{2\pi t} - 1}. $$

Switching the order of summation and integration, we get

$$ B(r, s) = 2 \int_{0}^{\infty} \left( \sum_{n=1}^{\infty} \binom{s}{n} e^{-\lambda_{n} r} \frac{(-it)^{n} - (it)^{n}}{2i} \right) \frac{dt}{e^{2\pi t} - 1}. \tag{4} $$

Step 3. The formula (4) is promising in the following sense: from Abelian theorems and binomial series, for $|t| < 1$ we get

\begin{align*} \lim_{r\downarrow 0} \sum_{n=1}^{\infty} \binom{s}{n} e^{-\lambda_{n} r} \frac{(-it)^{n} - (it)^{n}}{2i} &= \sum_{n=1}^{\infty} \binom{s}{n} \frac{(-it)^{n} - (it)^{n}}{2i}\\ &= \frac{(1-it)^{s} - (1+it)^{s}}{2i}. \end{align*}

Thus, if we extrapolate this result to all of $t > 0$ and ignore all the technical detail, we ansatz that

\begin{align*} B(0^{+}, s) &= 2 \int_{0}^{\infty} \frac{(1-it)^{s} - (1+it)^{s}}{2i} \frac{dt}{e^{2\pi t} - 1} \\ &= 2 \int_{0}^{\infty} \frac{\sin(-s \arctan t)}{(1+t^{2})^{-s/2}} \frac{dt}{e^{2\pi t} - 1} \\ &= \zeta(-s) + \frac{1}{s+1} - \frac{1}{2}, \tag{5} \end{align*}

where the last lit follows from the Abel-Plana formula. Consequently we get

$$ k! A_{k} = \left. \frac{d^{k}}{ds^{k}} B(0^{+}, s) \right|_{s=0} = (-1)^{k}(\zeta^{(k)}(0) + k!) $$

as claimed in (2). So it remains to choose a suitable sequence $(\lambda_{n})$ and justify the step between (4) and (5).

Justification?

I am currently working with the choice

$$ \lambda_{n} = \pi n^{2}. $$

In other words, I am considering Gaussian summability. Both heuristic calculations and numerical calculations are suggestive, but still the proof is not working well. I will update my answer as long as I find something new.

Answer 2

A partial answer:

The needed completion occurs, if I add -in the Ramanujan-summation-style- an integral of the base-function. For instance $$ \small \begin{array} {} \sum_{r=1}^\infty S1_{r,1} \cdot \zeta(-r) \underset{\mathcal N}{=} s_1 \approx -0.081 && C_1= \int_0^{-1} \log(1+t) dt = 1 && -\zeta'(0) = C_1 + s_1 \approx 0.9189 \\ \sum_{r=1}^\infty S1_{r,2} \cdot \zeta(-r) \underset{\mathcal N}{=} s_2 \approx -0.00635 && C_2= \int_0^{-1} \log(1+t)^2 dt = -2 && \zeta''(0) = C_2 + s_2 \approx -2.00635 \\ \vdots && \vdots && \vdots \end{array} $$ where again $S1_{r,c} = s1_{r,c} \cdot {c!\over r!}$ and $s1_{r,c}$ are the Stirling numbers first kind as described in the text of the question.

But the limits of the integrals are purely heuristic - I wouldn't know how to derive their values systematically...

Answer 3

(Adding information about the Noerlund-summation as asked for by @sos440 answer.)

Summations of divergent series, if they have alternating signs, can be done by summation-methods using infinite sized matrices. One example is the Euler-summation, which can be expressed by the "binomial" transform of a series. In matrix form this is done for instance this way.

I. Let $A$ be the column-vector containing the terms of a divergent series with alternating signs. The growthrate for that terms must not exceed geometrical growth, so the quotient $q$ of two consecutive term is allowed at most of constant absolute value.
With this we use two lower triangular matrices, first the matrix for partial summation, (I call it "Dr" in my Pari/GP-toolbox ) and we get $$ \operatorname{Dr} \cdot A = B $$ where the column-vector $B$ contains now the partial sums. After that, using the Pascalmatrix $P$, normed to have rowsums equal to 1, allow $$ \operatorname{RowNorm}(P) \cdot B = C $$ and the sequence of entries in $C$ might now converge to some finite value, which is taken as the Euler-Sum of the series described by $A$. It is optimal for such summations to have an adapted power of the matrix $P$, and what I actually do is to use the matrix-logarithm of $P$ and construct powers of it.
The logarithm, say $L$ of $P$ is just the matrix with the first subdiagonal containing the values $[1,2,3,4,..]$, and a general power of $P$, for instance the h'th power, is $ P^h = \exp(h \cdot L) $ so an Euler-sum of order $h$ is $$ \operatorname{RowNorm}(P^h) \cdot \operatorname{Dr} \cdot A = C $$ and I also include the dotproduct with the $Dr$ - matrix into one matrix-call in Pari/GP which is now my standard-use: $$ \operatorname{ESum}(h) \cdot A = C$$ which means an Eulersum to order $h$ of the series described by the columnvector $A$. Here the entries of $\small \operatorname{ESum}$ contain the final weights for the summation.

---

II. The weights for summations of higher orders in my studies are taken by the same scheme, where however the entries of the logarithm-matrix $L$ are taken to some power. For instance, if I use $ \small L_2 = \operatorname{SubDiag}([1,2^2,3^2,4^2,...]) $ then I get Noerlund-weights of order $2$, and in Pari/GP I write $ \small \operatorname{NoerSum}(o,h)$ where $o$ denotes now the exponent to which I take the $L$-matrix-terms. So I can do
$$ \operatorname{NoerSum}(2,1) \cdot A = C$$ where $A$ can now contain the factorials with alternating signs. With matrices of size of only, say, $32x32$ I get the following partial sums in $C$:

$\qquad $

where the first column shows the values to be summed, and the second column show the terms of $ \small C = \operatorname{NoerSum}(2,1.0) \cdot A$ which converge to the expected (divergent) sum of the alternating factorials.

Here is the top-left segment of the $\small \operatorname{NoerSum}(2,1)$-matrix:

$\qquad $

and here the weights without the dotproduct with $\small \operatorname{Dr}$:

$\qquad $

---

III. Finally, here is the sequence of partial sums, where I Noerlund-summed with the parameters (2,1) the first series in question, namely with the Stirlingnumbers 1st kind, scaled by the reciprocal factorials (of which is $\log(1+x)$ is the generating-function) : in the first column the symbolic description ($\zeta$ denoted by $z$), in the second column the numerical values of the terms of the series to be summed, and in the third column that final partial sums, taken by Noerlund-sum.

$\qquad $

(small remark: the parameters for the Noerlundsum could have been optimized, but I just left it here for comparable matrix-construction)

(You may ask for Pari/GP-code for reference if needed)

Answer 4

With product regularization I can atleast show the first one: $$n!=(n/e)^n*\sqrt{(2n\pi)}*\prod_{c=1}^{\infty}(1-c/n)$$

Derived from the product regularization of: $$\prod_{c=1}^{\infty}(1-c/n)=e^{\sum_{k=1}^{\infty} \frac{-\zeta(-k)}{kn^k}}$$ $$n!=(n/e)^n*\sqrt{(2n\pi)}*e^{\sum_{k=1}^{\infty} \frac{-\zeta(-k)}{kn^k}}$$

take n=1. $$e^{\sum_{k=1}^{\infty} \frac{-\zeta(-k)}{k}}=\frac{e}{\sqrt{(2\pi)}}$$ $${\sum_{k=1}^{\infty} \frac{-\zeta(-k)}{k}}=ln(\frac{e}{\sqrt{(2\pi)}})$$

The derivative of the zeta function is $$\zeta'(0)=-1/2ln(2\pi)$$ which you got, and the 1 you are missing is from the e. $${\sum_{k=1}^{\infty} \frac{-\zeta(-k)}{k}}=1+\zeta'(0)$$ The (-1)^k vanishes in the original formula because it's 1 at even integers so here you have. $${\sum_{k=1}^{\infty} \frac{\zeta(-k)}{k}}=-1-\zeta'(0)$$

About Product regularization, I think it's pretty helpful and does produce some usefull results for example. $$\frac{(1+1/n)^{n+1/2}}{e}=$$ $$\prod_{c=1}^{\infty}(1+c/(n+1))\prod_{c=1}^{\infty}(1-c/n)=e^{\sum_{k=1}^{\infty} \frac{\zeta(-k)}{k(n+1)^k}-\frac{\zeta(-k)}{kn^k}}=$$ $$\prod_{c=1}^{\infty}(1-\frac{c(c+1)}{n*(n+1)}=e^{\sum_{k=1}^{\infty} \sum_{j=0}^{k}\frac{\binom{k}{j}\zeta(-k-j)}{k((n+1)n)^k}}$$