Area of Validity of Writing an Exponential Integral as Sum of IntegralSinus and -Cosinus

Question

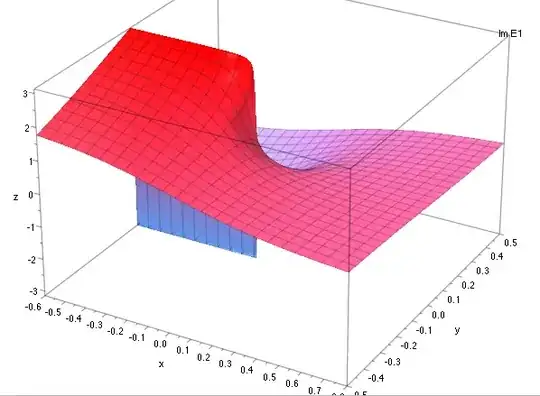
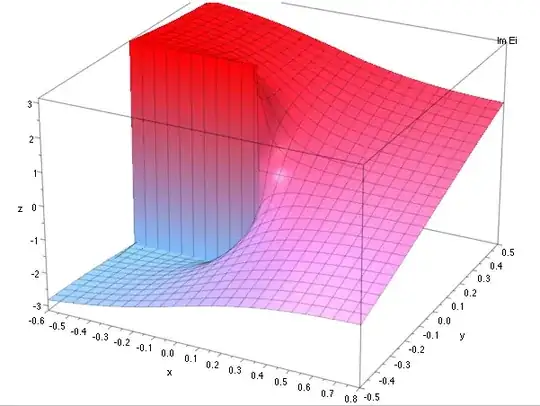
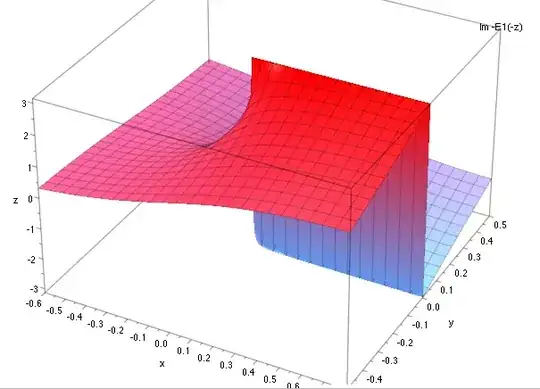
I'm confused by the two online references shown below. To me, they give different areas of validity of writing an exponential integral as sum of integralsinus and -cosinus.

On this Wiki page, I find the following:

Function ${\rm E}_1(z) = \int_1^\infty \frac {\exp(-zt)} {t} {\rm d} t \qquad({\rm Re}(z) \ge 0)$ is called exponential integral. It is closely related with ${\rm Si}$ and ${\rm Ci}$:

${\rm E}_1( {\rm i} x)= i\left(-\frac{\pi}{2} +{\rm Si}(x)\right)-{\rm Ci}(x) = i~{\rm si}(x) - {\rm ci}(x) \qquad(x>0)\;\;\;\;\;\;\;\;\;\;\;\; (1) $

As each involved function is analytic except the cut at negative values of the argument, the area of validity of the relation should be extended to ${\rm Re}(x) > 0$. (Out of this range, additional terms which are integer factors of $\pi$ appear in the expression).

Contrary, at least to my understanding, on Wolfram's page, I find:

The exponential integral of a purely imaginary number can be written $${\rm Ei}(ix)={\rm ci}(x) + i[\pi/2 + {\rm si}(x)]\;\;\;\;\;\;\;\;\;\;\;\; (2)$$ for $x>0$ and where ${\rm ci}(x)$ and ${\rm si}(x)$ are cosine and sine integral.

Despite their similarity, it might be that the two sites are not talking about the same thing, because adapting the relation ${\rm E}_1(x)=-{\rm Ei}(-x)$ for the argument $ix$ and applying it to $(2)$ gives: $$ \begin{eqnarray*} -{\rm Ei}(-ix)=-\left({\rm ci}(-x) + i\left[\pi/2 + {\rm si}(-x)\right]\right). \end{eqnarray*} $$ Further using

• ${\rm si}(x)={\rm Si}(z)-\pi/2$ [1] (they really write ${\rm Si}(z)$, but I think it's OK to put $x$ for $z$, right? ),

• ${\rm Si}(-x)=-{\rm Si}(x)$ [2] and

• ${\rm ci}(x)=_3{\rm Ci}(x)=_4{\rm Ci}(-x)$[3] [4],

I get $$ \begin{eqnarray*} -{\rm Ei}(-ix)&=&-\left({\rm ci}(-x) + i{\rm Si}(-x)\right)&&\\ &=&-\left({\rm Ci}(x) - i{\rm Si}(x)\right)&&\\ &=& i{\rm Si}(x)-{\rm Ci}(x)&\neq&{\rm E}_1( {\rm i} x). \end{eqnarray*} $$ So $(1)$ and $(2)$ don't match via my approach: $-i\frac{\pi}{2}$ is missing. I think I made a mistake somewhere and I still asume that they are talking about the same thing.

If not, I would be interested to know, why the area of validity is different in both cases. Or is Wikipedia wrong?

Answer 1

This is indeed a confusing subject. See Abramowitz and Stegun for the different kind of Exponential Integrals functions, relations between them and link with $\rm li$ function... $\rm E_n$ is a generalization of $\rm E_1$ (your definition of $E_1$ is $\rm E_n$ with $n=1$).
The links with ${\rm Si}$ and $\rm Ci$ are at page 232 (5.2.21 to 5.2.24).
The A&S was the reference for all these definitions for many years. More recent definitions may be found now online in the DLMF.

EDIT A simple way to choose between different interpretations is to consider the classical series expansion of $\rm E_1$ as the reference : $$\rm E_1(z)=-\gamma -\ln z -\sum_{n=1}^{\infty} \frac{(-z)^n}{nn!}\ \text{for}\ |{\rm arg}(z)|\lt \pi\ \ \text{(5.1.11)}$$

plot of the imaginary part of $\rm E_1$:

The $\rm Ein(z)=\int_0^z \frac{1-e^{-t}}{t} dt\ $ function removes the $-\gamma -\ln z$ part (and the associated 'branch problems') from $\rm E_1(z)$ to get an entire function.

Looking at WolframAlpha and functions.wolfram we may find the $\rm Ei$ formula : $$\rm{Ei}(z)=\gamma +\frac 12 \left(\ln z-\ln\frac 1z\right) +\sum_{n=1}^{\infty} \frac{z^n}{nn!}$$

plot of the imaginary part of $\rm {Ei}$ :

The formula for $\rm{Ei}(z)$ looks similar but is not $-\rm {E_1}(-z)$ as may be seen from the imaginary part of $-\rm {E_1}(-z)$ :

(to make things even more confusing $\rm{Ei}$ is sometimes defined as $-\rm {E_1}(-z)$ and conversely for example in the excellent book of Lebedev "Special functions and their applications")

The difference comes only from the choice of the cut : for $\rm{Ei}$ and $\rm {E_1}$ the cut was clearly chosen on the negative real axis (with continuity on the other side of course!) so that $-\rm {E_1}(-z)$ will have the cut on the wrong side.
The appropriate definition for $\rm{Ei}$ from $\rm {E_1}$ seems to be : $$ \rm{Ei}=\begin{cases} -\rm {E_1}(-z)+i\pi & \Im(z)>0\ \text{or}\ \Im(z)=0\ \text{and}\ \Re(z)>0\\ -\rm {E_1}(-z)-i\pi & \Im(z)<0\\ -\rm {E_1}(-z) & \Im(z)=0\ \text{and}\ \Re(z)<0\\ \end{cases} $$

I think that the $\rm{Ei}$ function verifies (in conformity with A&S) :
$\rm Ei(x)=-\rm E_1(-x)$ for $x\lt 0$ and real but
$\rm Ei(z)=-\rm E_1(-z)$ +/- $i\pi$ for the remaining cases (c.f. 5.1.7 and the $i\pi$ coming from the '$\ln z$' or Wolfram link where the incomplete gamma function $\Gamma(0,z)=\rm E_1(z)$),
$\rm Ei(ix)=\rm Ci(x)+i\ \rm Si(x) + i\pi/2$ for $x\gt 0$,
$\rm Ei(ix)=\rm Ci(x)-i\ \rm Si(x) - i\pi/2$ for $x\lt 0$ (for the more general formula see here),
$\rm si(z)=\rm Si(z)-\pi/2$,
$\rm Si(-z)=-\rm Si(z)$ but
$\rm Ci(-z)=Ci(z)+i\pi\ $ (or $-i\pi$ as in 5.2.20 depending of the branch of the $\ln z$ term in 5.2.16 or try Ci(-x)-Ci(x) at WolframAlpha).
(I used '$x$' for a real and '$z$' for a complex, in these documentations $x\gt 0$ and so on imply usually that x is real).

Again all this is easier to verify using series (for example $\ln i=i\pi/2$) :

$$\rm Ci(z)=\gamma+ \ln z +\sum_{n=1}^{\infty} \frac{(-1)^nz^{2n}}{(2n)(2n)!}\ \ \ \text{(5.2.16)} $$

$$\rm Si(z)=\sum_{n=1}^{\infty} \frac{(-1)^nz^{2n+1}}{(2n+1)(2n+1)!}\ \ \ \text{(5.2.14)} $$

Perhaps simply that MathWorld had the '$\rm si$ and '$\rm ci$' lower case instead of upper case... Anyway I think that the more reliable references are A&S (I didn't use much DLMF yet), functions.wolfram and WolframAlpha. Of course Wikipedia and MathWorld are great for cross-references!

Answer 2

I have some numerical code using expint of MATLAB. I cannot publish the code but I have strong evidence that there is a sign difference in the imaginary part. Matlab help claim that they calculate E1(x) but Ei(x)=-expint(-x)-i*pi so indeed: -expint(-1.8) ans = 4.249867557487933 + 3.141592653589793i

and Ei(1.8)=4.249...real

The split logarithm function 1/2(ln(x)-ln(1/x)) removes effectively the imaginary argument for negative reals. In calculation of expint MATLAB (ver 2012a) uses -log(z) yielding -i*pi for negative reals.

When I want to integrate -E1(-x) from x -inf to +abs(x) (the integral exp(t)/t) I think the integral should have the addition -i*pi considering that I move along the upper side of the real negative axis and then circulate origin from +pi to zero before progressing to abs(x). Therefore I reach an answer in line with your answer that we should indeed have: Ei(x)=-E1(-x)+i*pi but -expint(-1.8)+i*pi= 4.249867557487933 + 6.283185307179586i