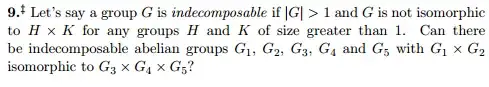This is answered in Theorem 90.1 of Infinite Abelian Groups (Vol II) by L. Fuchs, which shows that, for any $n\geq 2$, there is a finite rank abelian group which is the direct sum of two indecomposable groups and of $n$ indecomposable groups.
For the case $n=3$, one example that can be extracted from the general theorem is as follows. All the groups will be subgroups of $\mathbb{Q}^4$.
$G_1$ is generated by the elements $\left(\frac{2}{5^s},0,\frac{1}{5^s},0\right)$, $\left(0,\frac{2}{7^t},0,\frac{1}{7^t}\right)$ for all $s,t>0$ and $\left(0,0,\frac{1}{2},\frac{1}{2}\right)$.
$G_2$ is generated by the elements $\left(\frac{3}{5^s},0,\frac{1}{5^s},0\right)$, $\left(0,\frac{3}{7^t},0,\frac{1}{7^t}\right)$ for all $s,t>0$ and $\left(0,0,\frac{1}{3},\frac{1}{3}\right)$.
$G_3$ is generated by the elements $\left(\frac{1}{5^s},0,0,0\right)$ for all $s>0$.
$G_4$ is generated by the elements $\left(0,\frac{1}{7^t},0,0\right)$ for all $t>0$.
$G_5$ is generated by the elements $\left(0,0,\frac{1}{5^s},0\right)$, $\left(0,0,0,\frac{1}{7^t}\right)$ for all $s,t>0$ and $\left(0,0,\frac{1}{6},\frac{1}{6}\right)$.
It's straightforward to check that $G_1\oplus G_2=G_3\oplus G_4\oplus G_5$. Fuchs quotes a theorem from earlier in the book to prove indecomposability in the more general statement that he gives, but it's probably not too hard to check directly in this specific example.