The task is to complete the following Cayley table
for a given group. $e$ is of course the identity element. Together with group axioms and the fact that every Cayley table of a group must be a latin square, I arrived at
Is it correct? I know there is only one possible table and it sure looks like a latin square but I would appreciate if someone could confirm it's correct or not!
I agree with your answer.
Completing the Cayley table of order $6$ (if $pq=e$, it must be $qp=e$, etc.), you get a non commutative ($pr\ne rp$) magma, with identity element $e$.
Each element of it has unique inverse (each one is inverse of itself, but $p$ and $q$ mutually inverses).
Finally, if you relabel $e,p,q,r,s,t$ as $1,2,3,4,5,6$, you get the table
$$\begin{array}{c|cccccc} \cdot & 1 & 2 & 3 & 4 & 5 & 6\\ \hline 1 & \color{green}{1} & \color{red}{2} & \color{red}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ 2 & \color{red}{2} & \color{red}{3} & \color{green}{1} & \color{blue}{5} & \color{blue}{6} & \color{blue}{4}\\ 3 & \color{red}{3} & \color{green}{1} & \color{red}{2} & \color{blue}{6} & \color{blue}{4} & \color{blue}{5}\\ 4 & \color{blue}{4} & \color{blue}{6} & \color{blue}{5} & \color{green}{1} & \color{red}{3} & \color{red}{2}\\ 5 & \color{blue}{5} & \color{blue}{4} & \color{blue}{6} & \color{red}{2} & \color{green}{1} & \color{red}{3}\\ 6 & \color{blue}{6} & \color{blue}{5} & \color{blue}{4} & \color{red}{3} & \color{red}{2} & \color{green}{1} \end{array}$$
that you can check to be associative by using this brute-force Matlab script.
On the other hand, the above is a quasigroup since the Cayley table is a latin square and an associative quasigroup has identity element too.
I will try to construct the table in a systematic way. We know that in a group table each element appears exactly one in each row and each line. Also there must be an element where the corresponding row and line contains the same elements as the header row and line.
\begin{array}{c|cccccc} \cdot & e & p & q & r & s & t\\ \hline e & e & p & q & r & s & t\\ p & p & q & e & s & & \\ q & q & & & & & \\ r & r & & & e & & p\\ s & s & & & & & \\ t & t & & & & & \end{array}
To complete the $p$-line we use that a letter must appear exactly once in each line and each row. So we have $p t=r$ and $p s=t$, and we get
\begin{array}{c|cccccc} \cdot & e & p & q & r & s & t\\ \hline e & e & p & q & r & s & t\\ p & p & q & e & s & t & r \\ q & q & & & & & \\ r & r & & & e & & p\\ s & s & & & & & \\ t & t & & & & & \end{array}
$$p p=q \implies q x = (p p) x = p (p x)$$ so we can calculate the $q$-line.
\begin{array}{c|cccccc} \cdot & e & p & q & r & s & t\\ \hline e & e & p & q & r & s & t\\ p & p & q & e & s & t & r \\ q & q & e & p & t & r & s\\ r & r & & & e & & p\\ s & s & & & & & \\ t & t & & & & & \end{array}
We have $p =r t = \implies rp =r(rt)=(rr)t=et=t $ and so
\begin{array}{c|cccccc} \cdot & e & p & q & r & s & t\\ \hline e & e & p & q & r & s & t\\ p & p & q & e & s & t & r \\ q & q & e & p & t & r & s\\ r & r & t & & e & & p\\ s & s & & & & & \\ t & t & & & & & \end{array}
and from this we get the position of $s$ and $q$ because of the uniqueness of an element in a row and in a line
\begin{array}{c|cccccc} \cdot & e & p & q & r & s & t\\ \hline e & e & p & q & r & s & t\\ p & p & q & e & s & t & r \\ q & q & e & p & t & r & s\\ r & r & t & s & e & q & p\\ s & s & & & & & \\ t & t & & & & & \end{array}
We have $rq=s$, and so $sx=r(q(x))$, so the $s$-line can be generated from the $r$-line and the $q$-line, similar to the $q$-line. It should not be a problem to create the final line now. Either by the fact that $t=sq$, or by the fact the elements are exactly once in each row and column. So we end up with
\begin{array}{c|cccccc} \cdot & e & p & q & r & s & t\\ \hline e & e & p & q & r & s & t\\ p & p & q & e & s & t & r \\ q & q & e & p & t & r & s\\ r & r & t & s & e & q & p\\ s & s & r & t & p & e & q\\ t & t & s & r & q & p & e \end{array}
Now you still have to prove the associativity. But this is the group $D_3$, the Dihedral Group, which is the group of symmetry group of the equilateral triangle. It is also the group $S_3$, the group of permutation of three elements. We see this if we compare the Cayley Table. So we know that it will be associative.
But of course we want to prove associativity without referencing wiki. I think the simplest way to do this is to create the Cayley table of the symmetric operations of the equilateral triangle. This can be done rather quick.
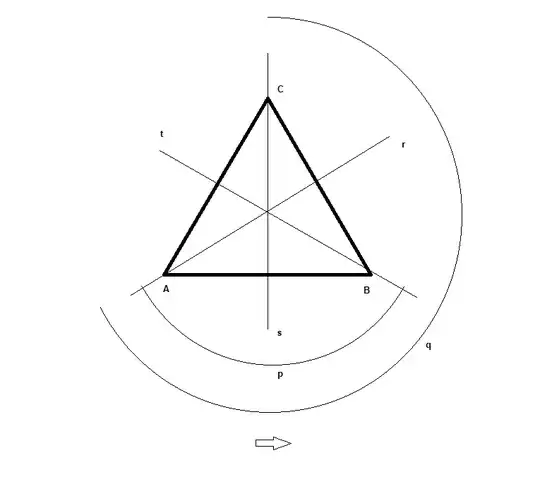
The reflection $r,s,t$ and the (counterclockwise) rotations $p,q$ are drawn in the sketch. The identity transformation is not shown. You have to check all 36 combinations. As an example we calculate $r\circ s$, to reflexions, will result in a rotation. Wich one? $s$ does not change $C$, but $r$ transforms $C$ to $B$, $q$ also transforms $C$ to $B$, so $r\circ s = q$. Doing this for the whole table we see that the table represents the binary operation $x\circ y$, where $\circ$ is the composition of function. We know that the composition of function is an associative operation, so our table is associative.
There are other ways to test associativity.
To test associativity you usually have to check all $6^3$ triples $a,b,c$ if $a(bc)=(ab)c$ holds. There are algorithms that may or may not reduce the number of checks (e.g. Light's associativity test
There are some special kind of tables where it is easy to prove associativity. So the subgroup of the elements $\{e,p,q\}$ defines such a special table. It is symmetric about the main diagonal therefore the operation is commutative. We have $q=p^2, e=p^3$ and so it is a cyclic group generated by $p$ and a cyclic group is always associative because of the properties of the exponents. Note that because of the commutativity of the operator the expression $p^3$ is not ambiguous, $(p^2)p$ and $p(p^2)$ give the same result.
In our case we also can prove the associativity with less then $6^3=216$ checks.
First we have to prove the following simple variants of the associativity law.
$$p^k p^n=p^{k-1}p^{n+1} \tag{1a}$$ $$(rp^k) p^n=(rp^{k-1})p^{n+1} \tag{1b}$$ $$p^k (p^nr)=p^{k-1}(p^{n+1} r) \tag{1c}$$ $$(rp^k) (p^nr)=(rp^{k-1}) (p^{n+1}r) \tag{1d}$$ $$r(rp^k)=p^k \tag{2}$$ and also the following $$rp^k=p^{-k}r \tag{3}$$
Note that by induction follows $$p^k p^n=p^{k+n} \tag{1'a}$$ $$(rp^k) p^n=rp^{k+n} \tag{1'b}$$ $$p^k (p^nr)=p^{k+n}r \tag{1'c}$$ $$(rp^k) (p^nr)=(rp^{k+n})r=r(p^{k+n}r) \tag{1'd}$$
Also note that the exponent $n$ is a number modulo $3$, so $-1$ is actually $2$ and $4$ is actually $1$.
How many checks do we have to do? To check statements $81a)$ we actually have nothing to check because this is the law of exponents we already mentioned befor. To check $(1b)$ we have to check $k=1,\ldots,3$ and $n=1,\ldots,3$, these are $9$ pairs of values. The same is true for $(1c)$ and $(1d)$. For $(2)$ and $3$ we have to check for $k=1,\ldots,3$. So all in all we have to do $33$ checks.
I leave these checks up to you.
Now we will prove the following $8$ equations.
$$(rp^k)((rp^m)(rp^n))=((rp^k)(rp^m))(rp^n) \tag{4a}$$ $$(p^k)((rp^m)(rp^n))=((p^k)(rp^m))(rp^n) \tag{4b}$$ $$(rp^k)((p^m)(rp^n))=((rp^k)(p^m))(rp^n) \tag{4c}$$ $$(rp^k)((rp^m)(p^n))=((rp^k)(rp^m))(p^n) \tag{4d}$$ $$(p^k)((p^m)(rp^n))=((p^k)(p^m))(rp^n) \tag{4e}$$ $$(p^k)((rp^m)(p^n))=((p^k)(rp^m))(p^n) \tag{4f}$$ $$(rp^k)((p^m)(p^n))=((rp^k)(p^m))(p^n) \tag{4g}$$ $$(p^k)((p^m)(p^n))=((p^k)(p^m))(p^n) \tag{4h}$$
Let's start with the prove of $(4a)$
$$(rp^k)((rp^m)(rp^n))=\text{(3)}\\ =(rp^k)((rp^m)(p^{-n}r))=\text{(1'd)}\\ =(rp^k)(r(p^{m-n}r))=\text{(3')}\\ =(rp^k)(r(rp^{n-m}))=\text{(2')}\\ =(rp^k)(p^{n-m})=\text{(1'b)}\\ =rp^{k-m+n}$$
In a similar manner $$((rp^k)(rp^m))(rp^n)\\=rp^{k-m+n}$$ can be shown. This completes the proof of $(4a)$.
The equations $(4b)$ to $(4g)$ can be proven in a similar manner. For $(4h)$ no proof is needed.
Now we have proven the associativity law
$$a(bc)=((ab)c$$ for every $a,b,c$, because $a,b,c$ are in $\{p^0, p^1, p^2, rp^0,rp^1,rp^2\}$
